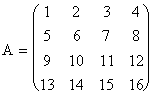
Si queremos definir la siguiente matriz en MATLAB:
entonces escribimos:
»A=[1 2 3 4;5 6 7 8;9 10 11 12;13,14,15,16];
(El simbolo "»" denota el prompt de MATLAB y no se escribe al entrar instrucciones). El ";" al final de la instrucción omite el "eco" o salida a la pantalla. La instrucción
»x=4:-1:1
general el vector fila x=[4,3,2,1]. La instrucción
»C=A(3:4,1:3);
se refiere a la submatriz
de A. También D=A([1,3],3:4) genera
En MATLAB podemos generar matrices especiales con las siguientes
instrucciones:
rand(n,m) - matriz
n´m de entradas aleatorias entre 0 y uno.
eye(n) - matriz identidad
n´n.
zeros(n,m) - matriz cero de tamaño
n´m.
ones(n,m) - matriz
n´m con todas las entradas uno.
Combinando estas instrucciones podemos generar matrices bastante complicadas.
Por ejemplo, la instrucción
»E=[eye(2),ones(2,3);zeros(2),[1:3;3:-1:1]]
genera la matriz
La instrucción round(x) redondea "x"
al entero más cercano a "x". Podemos combinar funciones en MATLAB.
Por ejemplo, round(10*rand(4)) genera una matriz
con entradas aleatorias entre 0 y 10.
Considere las siguientes matrices:
Entonces las operaciones A*B (producto matricial
de A con B), A+B (suma de A mas B),
3*A (multiplicación escalar de 3 por
A) tienen los siguientes resultados:
»A*B
ans =
16 19 13
10 11 7
»A+B
??? Error using ==> +
Matrix dimensions must agree.
»3*A
ans =
12 15
6 9
Note que MATLAB "anuncia" que A+B no se puede calcular. Las operaciones A' (transpuesto de A), inv(A) (inversa de A), y A^3 (esto es A*A*A) tienen como resultados:
»A'
ans =
4 2
5 3
»inv(A)
ans =
1.5000 -2.5000
-1.0000 2.0000
»A^3
ans =
174 235
94 127
Si precedemos las operaciones matriciales "*", "^" con el punto ".", entonces
estas se hacen termino a termino. Por ejemplo
A.*C y A.^2
generan:
» A.*C
ans =
-4 10
4 12
» A.^2
ans =
16 25
4 9
Considere le sistema lineal
Definimos la matriz de coeficientes y el lado derecho por las
instrucciones:
»A=[1 -2 3;4 1 -2;2 -1 4];
»b=[1 -1 2]';
Note el transpuesto en b para hacerlo un vector
columna. Vamos a resolver este sistema por tres métodos:
En el método de Gauss-Jordan, luego de obtener la forma echelon de
la matriz de coeficientes aumentada, eliminamos también la parte de
arriba de la matriz hasta producir una matriz donde las columnas con unos,
solo tienen un uno. Esto se conoce como la forma echelon reducida
(ver texto). Para comparar los tres métodos utilizamos la
instrucción flops de MATLAB que estima
el número de operaciones de punto flotante entre dos llamadas sucesivas
a flops. Una llamada de la forma
flops(0) inicializa el contador de operaciones
a cero. La sucesión de instrucciones:
» flops(0)
» x=A\b
x =
-0.0417
0.4167
0.6250
» flops
lleva a cabo eliminación Gaussiana en el sistema de arriba y produce como resultado:
ans =
73
esto es, se necesitaron aproximadamente 73 operaciones de punto flotante (sumas, restas, multiplicaciones ó divisiones) para resolver el sistema con eliminación Gaussiana. Para el método de Gauss-Jordan tenemos:
» flops(0)
» rref([A b])
ans =
1.0000 0 0 -0.0417
0 1.0000 0 0.4167
0 0 1.0000 0.6250
» flops
ans =
483
el cual requiere 483 operaciones de punto flotante. Finalmente el método de la inversa se realiza con la siguiente sequencia de instrucciones:
» flops(0)
» x=inv(A)*b
x =
-0.0417
0.4167
0.6250
» flops
ans =
108
el cual toma 108 operaciones. Vemos pues que eliminación Gaussiana
es el mejor de los tres métodos lo cual es cierto en general.
Usando MATLAB podemos estudiar la relación entre la solubilidad del
sistema Ax=b y la nosingularidad de la matriz de coeficientes A. En clase
vimos que el sistema Ax=b tiene solución única para cualquier
lado derecho b si y solo si la matriz A es nosingular. ¿Qué sucede
si A es singular? ¿Entonces Ax=b no tiene solución? Si A es singular
el sistema Ax=b puede tener solución para algunos b's pero de seguro
hay al menos un b* para el cual Ax=b* no tiene
solución. Vamos a genera una matriz singular con MATLAB:
» A=round(10*rand(6));
» A(:,3)=A(:,1:2)*[4 3]'
A =
2 5 23 9 7 3
0 8 24 8 9 6
7 0 28 5 8 8
7 1 31 1 3 10
9 5 51 7 0 4
4 7 37 4 7 2
(Como usamos la instrucción rand, el
resultado de esta y cualquier secuencia de instrucciones que use esta
función de MATLAB, no siempre será el mismo). La primera
instrucción genera una matriz aleatoria con entradas enteras entre
0 y 10, y con la segunda instrucción remplazamos la tercera columna
de A con cuatro veces la primera columna mas tres veces la segunda columna.
¡La matriz resultante es singular! (Explique esto sin calcular el
determinante). Generamos ahora un lado derecho arbitrario mediante la
instrucción:
» b=round(20*(rand(6,1)-0.5))
b =
10
4
5
3
-9
3
Esto genera una matriz 6´1 aleatoria con
entradas enteras entre -10 y 10. Resolvemos el sistema Ax=b calculando la
forma echelon reducida de la matriz de coeficientes aumentada
[A b]:
» rref([A b])
ans =
1 0 4 0 0 0 0
0 1 3 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
Como la última fila es de la forma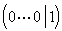 
el sistema
es inconsistente, i.e., no tiene solución. ¡Recuerde que A es
singular! Esto no quiere decir que Ax=b nunca tenga solución. Si definimos
c=A*b, con el b de arriba digamos, el sistema
Ax=c tiene solución x=b (¿por qué?). De hecho si calculamos
la forma echelon reducida de [A c] tenemos:
» c=A*b;
» rref([A c])
ans =
1 0 4 0 0 0 30
0 1 3 0 0 0 19
0 0 0 1 0 0 3
0 0 0 0 1 0 -9
0 0 0 0 0 1 3
0 0 0 0 0 0 0
el cual denota un sistema consistente dependiente con soluciones:
donde x3 es arbitrario.
MATLAB posee una gran cantidad de funciones matriciales. De las más
comunes tenenmos:
MATLAB provee excelentes funciones para gráficas en dos, tres y cuatro dimensiones. Veamos un par de ejemplos sencillos. Suponga que queremos trazar la gráfica de la función
Esto lo podemos lograr con las instrucciones:
» x=-5:.1:5;
» y=x.^2.*exp(-x.^2);
» plot(x,y)
La primera instrucción divide el intervalo [-5,5] en subintervalos
de largo 0.1, la segunda instrucción evalúa la función
en los puntos de la partición, y finalmente graficamos los resultados
con plot. La instrucción
plot tiene opciones para cambiar patrones del
trazado, poner titulos, etc.
Supongamos ahora que queremos dibujar la superficie:
Esto lo hacemos con la secuencia de instrucciones:
» x=-5:.4:5;
» y=x;
» [X,Y]=meshgrid(x,y);
» Z=X.^2.*exp(-Y.^2);
» surf(X,Y,Z)
Las primeras dos instrucciones dividen los ejes de "x" y "y" en subintervalos
de largo 0.4; la tercera instrucción genera una rejilla en el conjunto
[-5,5]´[-5,5] con cuadraditos de lados 0.4
como se ilustra en la siguiente figura:
La cuarta instrucción evalua la función en los puntos de la
rejilla, y finalmente trazamos la superficie con
surf.