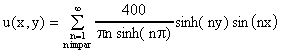Ecuación de Calor: Consideramos el problema de hallar la distribución de calor en una barra de largo L. El problema de frontera y valor inicial que describe esta situación es como sigue:

(A)

Primero hacemos un cambio de variables para transformar este problema a uno donde la A(t) y B(t) sean cero ambas. Definimos a este fin la función

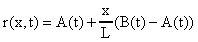
y v(x,t)=u(x,t)-r(x,t). Entonces v(x,t) es solución ahora del problema:

(B)

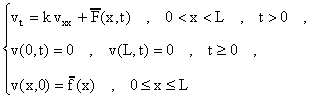
donde

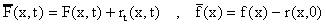
Ahora observamos que v(x,t)=w(x,t)+z(x,t) donde:

(C)

(D)

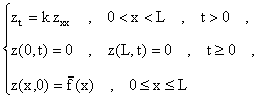
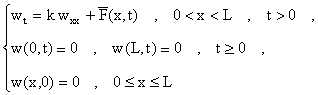
El problema para z(x,t) se resuelve primeramente buscando soluciones de la forma z(x,t)=X(x)T(t) y luego por el principio de superposición expresamos la solución final en terminos de una serie de Fourier. Los detalles se dieron en clase y resulta que

(SC)

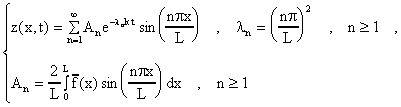
La función w(x,t) se busca usando transformadas de Fourier. Especificamente buscamos w(x,t) de la forma:

(SD)

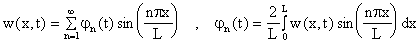
Note que esta w(x,t) formalmente satisface las condiciones de frontera en x=0,L. Si multiplicamos la ecuación diferencial de w(x,t) por , integramos en [0,L], usamos la ortogonalidad de las funciones , y simplificamos el termino con w_xx mediante integración por partes, obtenemos que para

(SD)

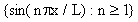
donde la condición inicial en 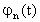viene de la condición inicial w(x,0)=0. Las soluciones (SC) y (SD) de (C) y (D) respectivamente se combinan mediante v(x,t)=w(x,t)+z(x,t) para obtener la solución de (B). Luego la solución de (A) queda dada finalmente por u(x,t)=v(x,t)+r(x,t). Cada uno de los problemas (B), (C), y (D) pueden ser resueltos individualmente por las formulas dadas.

Ejemplo: Considere el problema

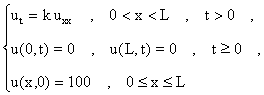
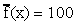
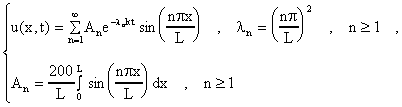
Este es un problema del tipo (C) donde . Tenemos pues que

Note que

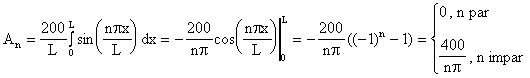
Sustituyendo en la fórmula de u(x,t) obtenemos

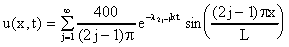
lo cual representa la solucion formal del problema dado.

Ecuación de onda: Las vibraciones libres de una cuerda atada a los extremos y de largo L esta dada por el problema de frontera y valor inicial:

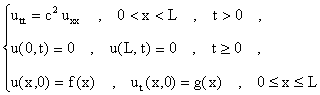
Aqui u(x,t) representa el desplazamiento vertical de la cuerda y f(x), g(x) el desplazamiento y velocidad inicial respectivamente. Al igual que para la ecuación de calor, podemos considerar las vibraciones forzadas donde aparece en la ecuación diferencial un termino nohomogeneo F(x,t). La derivación de las ecuaciones en este caso es similar a la de la ecuación de calor y la dejamos como ejercicio. En forma similar al problema (C) arriba, buscamos soluciones de este problema de la forma u(x,t)=X(x)T(t) y luego por el principio de superposición expresamos la solución final en terminos de una serie de Fourier. Los detalles los dimos en clase y resulta que:

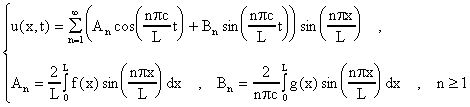
Ejemplo: Halle el movimiento para todo "t" de una cuerda de largo L atada a los extremos donde el desplazamiento y velocidad inicial estan dados por:

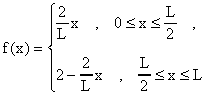
y g(x)=0. Mostramos aqui la gráfica de f(x) para el caso L=1:

Tenemos ahora que B_n=0 para toda n y que

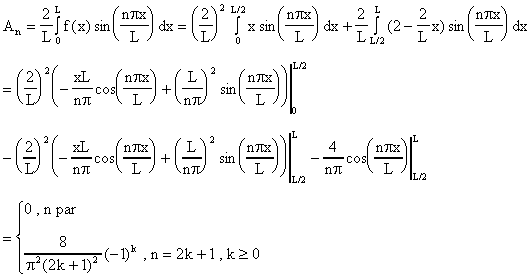
La solución u(x,t) esta dada pues por la serie:

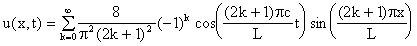
Ecuación de Laplace: Consideramos ahora el problema de frontera que describe la temperatura en equilibrio de una placa rectangular. Si u(x,y) denota la temperatura de la placa entonces u(x,y) satisface el siguiente problema de frontera:

donde las g's son funciones dadas que representan la temperatura en los bordes de la placa. Buscamos soluciones separables de la forma u(x,y)=X(x)Y(y). Tenemos pues

de donde se obtiene que:

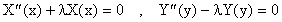
Considere el caso en que g₃(y)=0=g₄(y). Entonces X(0)=0=X(L) y de la ecuación diferencial de X(x) obtenemos que:

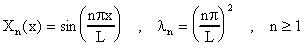
Ahora de la ecuación de Y(y) y usando el valor de l_n tenemos que:

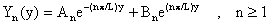
Usando ahora el principio de superposición, buscamos soluciones u(x,y) de la forma:

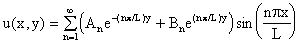
Las constantes A_n, B_n se determinan usando las condiciones u(x,0)=g₁(x) y u(x,H)=g₂(x).

Ejemplo: Tomamos el caso L=H=p y g₁(x)=0. Entonces la condición u(x,0)=0 implica

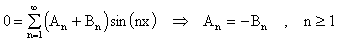
Asi que

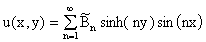
Ahora u(x,p)=g₂(x) implica que

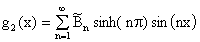
es decir

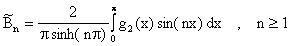
Si tomamos digamos g₂(x)=100, entonces

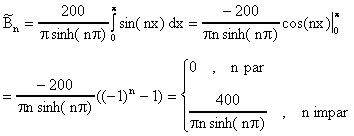
Asi que