| Hogar | Suscripciones | Números anteriores | Créditos | Escríbanos | CUH | Matemáticas |

| Año 3, número 1 | 25 de enero de 2002 |
ARTÍCULO MP3: El Formato de Audio Que Hizo Práctica la Distribución de Música por INTERNET 25 de enero de 2002 (José O. Sotero Esteva)
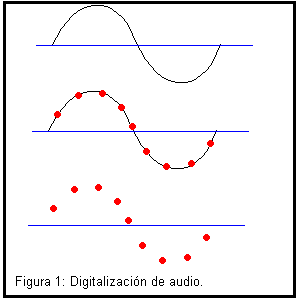
Señales de audio digitales El sonido (análogo) puede ser representado como una curva en el plano t/x que típicamente fluctúa sobre y bajo el eje de t. Aquí la x representa tiempo y la y intensidad. Una curva sinusoidal podría ser un ejemplo de una curva que representa un sonido. Mientras más alta la frecuencia (menor el periodo) de esa curva el sonido se percibe más agudo. En su forma más sencilla la representación de audio digital consiste en una sucesión de números binarios representando las coordenadas de y de esa curva para una sucesión de t´s equidistantes una de la próxima. La tasa de muestreo, usualmente medida en herzios, es una medida de cuan cercanas están esas t´s. Un CD de música tiene un muestreo típico de 16 bits a una tasa de muestreo de 44.1 kHz. Esto quiere decir que cada y se mide con un número de 16 bits y que para el muestreo se usan 44,100 t´s en cada intervalo de un segundo. Así una canción de cuatro minutos en estereo requiere cerca de 40 megabytes (MB) para ser grabada. Podemos llegar a este número calculando = 2 bytes * 2 canales * 41,100 / seg / canales * 240 seg = 39,456,000 bytes = 39.456 MB.
Pero todo usuario de INTERNET sabe que descargar un archivo de 40 MB no es un asunto menudo. Así que si queremos implantar un servicio de distribución de música como lo era Napster tenemos que encontrar una mejor manera de codificar esa información de modo que los archivos resultantes sean más pequeños. MP3: Un formato de compresión de audio MP3 son las siglas que se usan para referirse a ¨MPEG Audio Layer-3¨. En este formato se divide el proceso de compresión en 3 capas que logra comprimir el sonido codificado originalmente en un CD por un factor de 12 sin perder calidad de sonido. Incluso cuando se usan factores de compresión mayores de 24 se mantiene un sonido de buena calidad mediante el uso de un proceso llamado codificación perceptual. Dos de las capas de MP3 están basadas en procedimientos de la matemática computacional: transformada rápida de Fourier y códigos de Huffman. La Transformada Rápida de Fourier La Transformada rápida de Fourier es un algoritmo para producir coeficientes de la Transformada Discreta de Fourier, y esta última es una versión discreta de la transformada continua (TCF). La TCF es útil para representar curvas periódicas mediante la serie: Pero el insumo de un codificador de MP3 no es la señal análoga del audio. No es una curva contínua. Es la señal digitalizada. Por suerte existe una versión discreta de la suma: Si fueramos a calcular la TDF tal y como aparece en la fórmula nos tomaria tiempo O(n2). El FFT es un algoritmo que computa la TDF en O(n log(n)) y a su existencia le debemos agradecer que no necesitemos computadoras demasiado poderosas para oir MP3s. Códigos de Huffman Aparentemente las sucesiones de XXX números que salen del FFT no están uniformemente distribuidos. Aquí entran, entonces, los códigos de Huffman que son muy eficaces al comprimir información en la que algunos símbolos son más frecuentes que los demás. Para visualizar el algoritmo de que produce los códigos de Huffman imaginemos que queremos comprimir un texto en vez de sonido. Los archivos de texto suelen ser un buen ejemplo de un tipo de archivo en el cual los códigos de Huffman son buenos. Las letras no se usan con la misma frecuencia en los lenguajes. Por ejemplo, en el lenguaje español la letra e se usa con mucha más frecuencia que la x. Para comprimir con este método se construye un código, una tabla de equivalencias, para cada archivo que se va a comprimir. Contrario al código ASCII que siempre usa ocho bits para codificar cada letra, un código de Huffman puede usar dos bits para codificar una letra y ocho para codificar otra. El truco que logra Huffman que la representación de dos bits se use para representar símbolos, letras en nuestro ejemplo, que son más frecuentes que la letra representada por los ocho bits economizando así espacio de almacenamiento.
Epílogo Hemos visto cómo dos técnicas de la matemática computacional se han combinado para producir un formato de representación de sonido que nos permite, entre otras cosas, intercambiar música a través de la INTERNET. Los corolarios técnicos y sociales de este aparente pequeño desarrollo técnico son interesantísimas. Eso quizás sea materia para otro MC++. | |
 (Basado en parte de la charla dictada en el Seminario de Matemáticas Computacionales de la UPRH)
(Basado en parte de la charla dictada en el Seminario de Matemáticas Computacionales de la UPRH)
 Si estamos usando un disco óptico con cerca de 500 MB de capacidad para almacenar
la música eso quiere decir que caben como 12 canciones. Un equipo con un bus de una capacidad
de 100 MB / seg y un procesador barato son suficientes para transmitir y procesar esa información
en tiempo real.
Si estamos usando un disco óptico con cerca de 500 MB de capacidad para almacenar
la música eso quiere decir que caben como 12 canciones. Un equipo con un bus de una capacidad
de 100 MB / seg y un procesador barato son suficientes para transmitir y procesar esa información
en tiempo real.
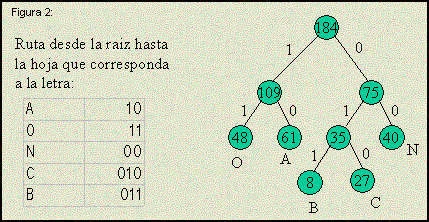 A modo de ejmplo considere un texto que olo use cinco letras y
que la frecuencia con la que aparecen en el texto es: 61 A, 48 O, 40 N, 27 C y 8 B.
Para crear un código para este texto se ordenan las frecuencias de mayor a menor. Con las
últimas dos se forma el subarbol con raiz 35 (= 27 + 8) del arbol de la figura 2.
Las entradas correspondientes a la C y la B se sustituyen en la lista por 35 y se repite el proceso:
se ordena, se toman los últimos dos y se forma el sobarbol con raiz 75. El código de Huffman de cada
letra se obtiene uniendo las etiquetas de las aristas desde la raiz hasta la hoja correspondiente a la letra.
Aunque este ejemplo es algo pequeño para ilustrar de manera realista el rendimiento de este algoritmo
note que la palabra BANCO que ocuparía 8 * 5 = 40 bits si se codifica en ASCII ocupa 12 bits en este
código.
A modo de ejmplo considere un texto que olo use cinco letras y
que la frecuencia con la que aparecen en el texto es: 61 A, 48 O, 40 N, 27 C y 8 B.
Para crear un código para este texto se ordenan las frecuencias de mayor a menor. Con las
últimas dos se forma el subarbol con raiz 35 (= 27 + 8) del arbol de la figura 2.
Las entradas correspondientes a la C y la B se sustituyen en la lista por 35 y se repite el proceso:
se ordena, se toman los últimos dos y se forma el sobarbol con raiz 75. El código de Huffman de cada
letra se obtiene uniendo las etiquetas de las aristas desde la raiz hasta la hoja correspondiente a la letra.
Aunque este ejemplo es algo pequeño para ilustrar de manera realista el rendimiento de este algoritmo
note que la palabra BANCO que ocuparía 8 * 5 = 40 bits si se codifica en ASCII ocupa 12 bits en este
código.