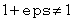 .
.
Introducción a MATLAB
¿Cómo Empezar?
Entrando Matrices Simples
MATLAB trabaja esencialmente con
matrices numéricas rectangulares. La manera más
fácil de entrar matrices pequeñas es enumerando
los elementos de ésta de tal manera que:
Ejemplo:
A
= [ 1 2 3; 4 5 6; 7 8 9 ]
resultaría en la matriz
A =
1 2 3
4 5 6
7 8 9
MATLAB guarda esta matriz para utilizarla
luego bajo el nombre de A.
Si la matriz a entrar es muy grande
se puede utilizar el siguiente formato:
A = [1 2 3
4 5 6
7 8 9]
El comando load
y la función fread
pueden leer matrices generadas en sesiones anteriores ó
generadas por otros programas.
Elementos de matrices
Los elementos de una matriz pueden
ser cualquier expresión de MATLAB.
Ejemplo:
x
= [-1.3,sqrt(3),(1+2+3)
*4/5]
resultaría
en
x =
-1.3000 1.7321 4.8000
Nos podemos referir a elementos individuales
de la matriz con índices entre paréntesis.
Ejemplo: En el ejemplo anterior
x(5)
= abs(x(1))
resultaría
en
x =
-1.3000 1.7321 4.8000 0
1.3000
Para añadir otra fila a la
matriz A de arriba podemos hacer lo siguiente:
r
= [10 11 12];
A = [A; r]
y
resultaría en
A =
1 2 3
4 5 6
7 8 9
10 11 12
Instrucciones de MATLAB
y Variables
Si omites el nombre de la variable
y el signo "=", MATLAB automáticamente crea la
variable ans
para guardar el resultado. También distingue las letras
mayúsculas de las minúsculas. Todos los nombres
de funciones deben ser en letras minúsculas.
Obteniendo Información
del Espacio de Trabajo
Los ejemplos que hemos dado se han
guardado en variables que están en el espacio de trabajo
de MATLAB. Para listar las variables en el espacio de trabajo
se utiliza el comando who.
Para ver información adicional acerca de estas variables
se utiliza el comando whos.
Variables Permanentes
Las variables permanentes
son aquellas con significado especial, y que no se pueden eliminar.
Estas son por ejemplo las variables ans
y eps.
La variable eps
es una tolerancia para determinar cosas como singularidad y rango.
Su valor inicial es la distancia de 1.0 al próximo número
de punto flotante mayor. En otras palabras, eps
es el número positivo más pequeño tal que
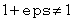
Ayuda
Para obtener ayuda ó información
de MATLAB utilice el comando help.
Saliendo y Guardando el
Espacio de Trabajo
Para salir de MATLAB se escribe quit
ó exit.
Al terminar una sesión de MATLAB, las variables en el
espacio de trabajo se borran. Si deseas guardar tu espacio de
trabajo escribes save.
save
guarda todas las variables en un archivo llamado matlab.mat.
Se puede utilizar save
y load
con otros nombres de archivos, ó para guardar solo variables
seleccionadas
Ejemplo:
save
temp X Y Z
Este ejemplo guarda las variables
X, Y, Z en el archivo temp.mat.
Usando el comando load temp
las obtienes nuevamente del archivo temp.mat.
load
y save
también pueden importar y exportar información de
archivos ASCII.
Expresiones Numéricas
y Aritméticas
Puedes construir expresiones con
los operadores usuales de aritmética y reglas de precedencia:
+ suma
- resta
* multiplicación
/ división a la derecha (división
usual)
\ división a la izquierda
^ exponenciación
Algunas funciones matemáticas
elementales de MATLAB son abs,
sqrt,
log
y sin.
Puedes añadir funciones fácilmente con los archivos-M.
La función intrínseca
pi
devuelve el número . La función Inf
equivale a "infinito".
Matrices y Números
Complejos
MATLAB también permite números
complejos, indicados por las variables especiales i
y j,
en todas sus operaciones y funciones.
Funciones
Las funciones que utiliza MATLAB
son intrínsecas al procesador de éste. Otras funciones
están disponibles en la librería externa de archivos-M.
Además de éstas funciones todo usuario también
puede crear otras funciones. Puedes combinar las funciones de
acuerdo a tu necesidad.
Ejemplo:
x
= sqrt(log(z))
Operaciones de Matrices
Matrices Transpuestas
El caracter ' (apóstrofe)
denota la transpuesta de la matriz. Si tenemos la matriz A y
llamamos B = A', B es la transpuesta de la matriz A.
Sumando y Restando Matrices
Las operaciones suma (+) y resta
(-) son definidas para las matrices siempre y cuando éstas
tengan la misma dimensión. Es decir, si A y B son matrices
3 x 3, entonces A + B se puede calcular.
Suma y resta también está
definidos si uno de los operandos es un escalar, es decir, una
matriz 1 x 1.
Ejemplo:
x =
-1
0
2
y = x - 1
resultaría
en
y =
-2
-1
1
Multiplicando Matrices
La operación de multiplicación
de matrices está definida siempre que el número
de columnas de la primera matriz sea igual a el número
de filas de la segunda matriz.
El producto interior (producto escalar
ó producto punto) se consigue de la siguiente manera:
x'
*
y
asumiendo que x
y y son
vectores columnas. Note que y'
* x
produce el mismo resultado.
El producto de una matriz y un vector
es un caso especial del producto matriz-matriz y naturalmente,
un escalar como pi,
puede multiplicar, ó ser multiplicado por, cualquier matriz.
Dividiendo Matrices
En división de matrices,
si A es una matriz cuadrada no-singular, entonces A\B y B/A corresponden
a la multiplicación izquierda y derecha de B por el inverso
de A, esto es, inv(A) * B y B * inv(A) respectivamente. El resultado
es obtenido directamente sin la computación del inverso.
X = A\B es una solución a A * X = B
X = B/A es una solución a
X * A = B
A\B es definido cuando B tiene la
misma cantidad de filas que A. Si A es cuadrada, el método
usado es Eliminación Gaussiana. El resultado es una matriz
X con las mismas dimensiones que B.
Si A no es cuadrada, se factoriza
utilizando la ortogonalización de Householder con pivoteo
de columnas. Los factores son usados para resolver sistemas de
ecuaciones sub-determinados y sobre-determinados. El resultado
es una matriz X m-por-n donde m es el número
de columnas de A y n es el número de columnas de
B. Cada columna de X tiene, al menos, k componentes diferentes
de cero, donde k es el rango efectivo de A.
B/A esta definido en términos
de A\B por B/A = (A'\B') '.
Usando Exponentes con Matrices
La expresión A^n eleva A a
la n-ésima potencia y esta definido si A es una matriz
cuadrada y n un escalar.
Funciones Matriciales Trascendentales
y Elementales
MATLAB considera expresiones como
exp(A)
y sqrt(A)
como operaciones de arreglos, definidas en los elementos individuales
de A. También puede calcular funciones trascendentales
de matrices, como la matriz exponencial y la matriz logarítmica.
Estas operaciones especiales están definidas solamente
para matrices cuadradas.
Otras funciones elementales de matrices son:
poly
- polinomio característico
det
- determinante
trace
- traza
kron
- producto tensorial de Kronecker
eig
- calcula los valores
propios de la matriz
Operaciones de Arreglos
El término operaciones
de arreglo se refiere a las operaciones de aritmética
elemento por elemento. Un punto (.) antes de un operador indica
una operación de arreglos elemento por elemento.
Suma y Resta de Arreglos
Para suma y resta, las operaciones
de arreglos y las operaciones de matrices son iguales.
Multiplicación y
División de Arreglos
El símbolo .* denota multiplicación
de arreglos elemento por elemento.
Ejemplo:
x
= [1 2 3]; y = [4 5 6];
z
= x. *y
resulta en
z
=
4 10 18
Las expresiones A./B y A.\B dan los
cocientes de los elementos individuales.
Ejemplo:
z
= x.\y
resulta
en
z =
4.0000 2.5000 2.0000
Exponentes con Arreglos
El símbolo .^
denota exponenciación
elemento por elemento.
Operadores de Relacionales
Hay seis operadores relacionales disponibles para comparar dos matrices de igual dimensión.
< menor que
<= menor que ó igual
> mayor que
>= mayor que ó igual
== igual que
~= no igual que
Operadores Lógicos
Los operadores &, | y ~ son los
operadores de lógica "y", "ó"
y "no" respectivamente.
El resultado de C = A & B es
una matriz cuyos elementos son unos donde A y B sean ambos distintos
de cero, y ceros donde A ó B sean cero. A y B deben de
ser matrices con las mismas dimensiones, a menos que una de ellas
sea un escalar.
El resultado de C = A | B es una
matriz cuyos elementos son unos donde A ó B tienen un elemento
diferente de cero, y ceros donde ambas tienen elementos cero.
A y B deben de ser matrices con las mismas dimensiones, a menos
que una sea un escalar.
El resultado de B = ~A es una matriz
cuyos elementos son uno donde A tiene un elemento cero, y ceros
donde A tiene elementos diferentes de cero.
La función any(x) devuelve 1 si cualquiera de los elementos de x es diferente de cero, de lo contrario devuelve 0. La función all(x) devuelve 1 solamente si todos los elementos de x son diferentes de cero. Estas funciones se usan en cláusulas if. Por ejemplo:
if all(A <.5)
. . .
end
Para argumentos matriciales, any
y all
trabajan por columnas para devolver un vector fila con el resultado
para cada columna. Aplicando la función dos veces, any(any(A)),
siempre reduce la matriz a una condición escalar.
Las funciones relacionales y lógicas
en MATLAB son:
any
- condiciones lógicas
all
- condiciones lógicas
find
- halla índices de arreglos de valores lógicos
exist
- verifica si existen variables
isinf
- detecta infinitos
finite
- verifica para los valores finitos
Funciones Matemáticas
Algunas funciones trigonométricas
utilizadas por MATLAB son:
sin
- seno
cos
- coseno
tan
- tangente
asin
- seno inverso
acos
- coseno inverso
atan
- tangente inversa
Algunas funciones elementales son:
abs
- valor absoluto ó
magnitud compleja
sqrt
- raíz cuadrada
real
- parte real
imag
- parte imaginaria
conj
- conjugado complejo
round
- redondeo al entero
más cercano
fix
- redondeo hacia cero
floor
- redondeo hacia -
ceil
- redondeo hacia
sign
- función signo
exp
- exponencial base
e
log
- logaritmo natural
log10
- log base 10
También hay funciones especiales
como las de bessel,
gamma y
beta.
Manipulación de
Vectores y Matrices
Generando Vectores
Los dos puntos, :,
son importantes en MATLAB. Por ejemplo
x
= 1:5
genera un vector fila que contiene
los números enteros del 1 al 5:
x
=
1 2 3 4 5
No necesariamente se tiene que incrementar
por números enteros, pueden ser decimales, números
negativos ó constantes.
Índices
Podemos referirnos a elementos individuales
de matrices encerrando sus índices en paréntesis.
Ejemplo:
A
=
1 2 3
4 5 6
7 8 9
A(3, 3) = A(1, 3) + A(3, 1)
resultaría
en
A =
1 2 3
4 5 6
7 8 10
Un índice puede ser un vector.
Si x
y v
son vectores, entonces x(v)
es [x(v(1)), x(v(2)), ...,
x(v(n))]. Para matrices,
los índices de vectores permiten acceso a submatrices contiguas
y no-contiguas. Por ejemplo, suponga que A es una matriz 10 por
10. Entonces
A(1:5,
3)
especifica la submatriz 5 x 1, ó
vector columna, que consiste de los primeros cinco elementos en
la tercera columna de A. También
A(1:5,
7:10)
es la submatriz 5 x 4 de las primeras
cinco filas y las últimas cuatro columnas.
Utilizando solo los dos puntos denota
todo lo correspondiente a la fila ó columna. Podríamos
tener una instrucción como:
A(:,
[3 5 10]) = B(:, 1:3)
que reemplaza la tercera, quinta
y décima columna de A con las primeras tres columnas de
B.
Manipulación de
Matrices
Funciones de Matrices
Existen varias factorizaciones de
matrices que mencionamos brevemente y luego se discutirán
en clase.
La Factorización Triangular
ó Factorización LU expresa cualquier
matriz cuadrada como el producto de dos matrices triangulares.
Esta factorización se utiliza para obtener el inverso
y el determinante. También es la base para la solución
de sistemas lineales. Para obtener la factorización LU
de A escribimos, [L, U] =
lu(A).
La Factorización Ortogonal
ó Factorización QR se utiliza para matrices
cuadradas ó rectangulares. Esta factorización se
utiliza para resolver sistemas lineales con más ecuaciones
que desconocidas. Esta factorización también es
la base para las funciones null
y orth,
que generan bases ortonormales para el espacio nulo y rango de
una matriz rectangular dada.
La Descomposición de Valores
Singulares es importante para el análisis de problemas
que envuelvan matrices. La asignación triple [U, S, V]
= svd(A) produce los tres factores en la descomposición
de valores singulares A = U*S*V'. Las matrices U y V son ortogonales
y la matriz S es diagonal. La función svd(A)
devuelve solamente los elementos de la diagonal de S, que son
los valores singulares de A.
La Descomposición de Valores
Propios se utiliza para obtener los valores y vectores propios
de una matriz cuadrada A. La función eig(A)
devuelve los valores propios de A en un vector columna. La asignación
[X,D]=eig(A)
produce una matriz diagonal D cuyos elementos diagonales son los
valores propios de A y las columnas de X son los vectores propios
correspondientes.
Las Funciones de norma, rango
y acondicionamiento asociadas son:
cond
- número de condición en la norma 2
norm
- norma 1, norma 2, norma F, norma
rank
- rango
rcond
- estimado del número de condición
Funciones de Funciones
MATLAB representa funciones matemáticas
mediante archivos-M de tipo función. Un ejemplo de una
función es el archivo-M llamado humps.m.
Ejemplo: El archivo-M llamado humps.m
contiene las siguientes instrucciones:
function
y = humps(x)
y = 1./((x-.3).^2 +.01) + 1./((x-.9).^2
+.04) - 6;
y para la gráfica de la función
escribimos
x
= -1:.01:2;
plot(x, humps(x))
lo cual produce la gráfica
Integración Numérica
(Cuadratura)
El área bajo la gráfica
de la función f(x) se puede aproximar integrando f(x) numéricamente
mediante una regla de cuadratura. Para integrar la función
definida por humps.m
desde 0 hasta 1 escribimos:
q
= quad('humps',
0, 1)
q =
29.8583
Note que el argumento de quad
contiene un nombre de una función. Por esto quad
se llama una función de función, i.e., es
una función que opera en otras funciones.
Ecuaciones No-lineales
y Funciones de Optimización
Las funciones de funciones para ecuaciones
no-lineales y optimización incluyen:
fmin
- mínimo de una función de una variable
fmins
- mínimo de una función multi-variable (minimización
no-lineal sin restricciones)
fzero
- cero de una función de una variable
constr
- minimización con restricciones
fsolve
- solución de ecuación no-lineal
leastsq
- cuadrados mínimos
no-lineales
Funciones para Ecuaciones
Diferenciales
Las funciones de MATLAB para resolver
problemas de valor inicial para ecuaciones diferenciales ordinarias
son:
ode23
- método Runge-Kutta
de largo de paso variable que combina un método de orden
dos con uno de orden tres.
ode45
- método Runge-Kutta-Fehlberg
de largo de paso variable que combina un método de orden
cuatro con uno de orden cinco.
Gráficas
Gráficas en Dos
Dimensiones
Funciones Elementales para Graficar
plot
- crea una gráfica de vectores ó columnas de matrices.
loglog
- crea una gráfica utilizando una escala logarítmica
para ambos ejes.
semilogx
- crea una gráfica utilizando una escala logarítmica
para el eje-x y una escala lineal para el eje-y.
semilogy
- crea una gráfica utilizando una escala logarítmica
para el eje-y y una escala lineal para el eje-x.
Puede añadir títulos,
encabezamientos de ejes, líneas entre cortadas y texto
a tus gráficas utilizando:
tittle
- añade título a la gráfica
xlabel
- añade encabezamiento al eje-x
ylabel
- añade encabezamiento al eje-y
text
- añade una cadena de texto en una localización
específica
gtext
- añade texto a la gráfica utilizando el ratón
grid
- crea líneas entrecortadas
Creando una gráfica
Si y es un vector, plot(y)
produce una gráfica lineal de los elementos de y versus
el índice de estos. Si especifica dos vectores como argumentos,
plot(x, y)
produce una gráfica de y versus x.
Graficando Matrices
plot(Y)
dibuja una línea para cada columna de Y. El eje-x
es encabezado por el vector índice de fila, 1:m,
donde m
es el número de filas en Y.
Si plot
es usado con dos argumentos y si X ó Y tienen más
de una fila ó columna, entonces:
si Y es una matriz, y x es un vector, plot(x,Y) grafica las filas ó columnas de Y versus el vector x;
si X es una matriz y y es un vector, plot(X,y) grafica cada fila ó columna de X versus el vector y;
si X y Y son ambas matrices del
mismo tamaño, plot(X,
Y) grafica las columnas
de X versus las columnas de Y.
También puedes usar la función
plot
con múltiples pares de argumentos de matriciales:
plot
(X1, Y1, X2, Y2, ...)
Cada par X-Y es graficado, generando
líneas múltiples. Los pares diferentes pueden ser
de dimensiones diferentes.
Importando Datos
Puede importar y graficar datos generados
fuera de MATLAB utilizando el comando
load.
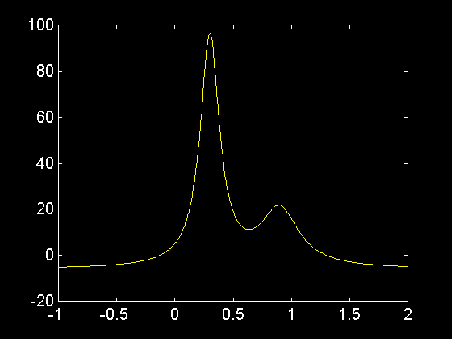
Graficando Funciones Matemáticas
Hay diferentes maneras de graficar
funciones y = f(x). Una de estas formas es evaluar la función
en miles de puntos en el intervalo de interés. La siguiente
función oscila infinitamente rápido en el intervalo,
0 x 1. Podemos gráficarla como sigue:
x
= (0:1/2000:1)';
plot(x, cos(tan(pi*x)))
lo cúal produce la gráfica:
Para hacer esto más eficiente
podemos usar la función fplot
la cual concentra su evaluación sobre las regiones donde
la rapidez de cambio de la función es más grande.
Para evaluar una función, se crea un archivo de esta función y se le pasa el nombre del archivo a fplot. El siguiente archivo-M de tipo función define la función anterior como fofx.
function
y = fofx(x)
y = cos(tan(pi*x));
Este archivo se guarda con el nombre
de fofx.m.
Ahora la instrucción
fplot('fofx',
[0 1])
produce la gráfica
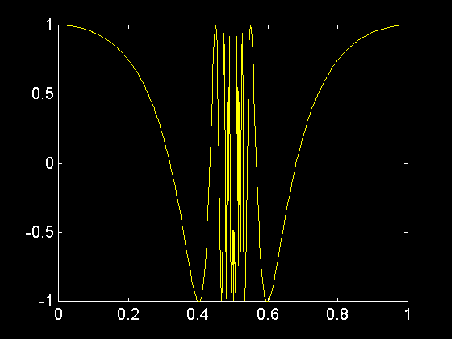
Aquí, fplot
usa menos puntos para evaluar la misma función a intervalos
más cerrados en la región donde la rapidez de cambio
es mayor.
Control de Flujo
Ciclos FOR
El ciclo FOR
permite que una instrucción, ó grupo de instrucciones,
pueda repetirse un número determinado de veces. Por ejemplo,
for
i = 1:n, x(i) = 0, end
asigna 0 a los primeros n elementos
de x. Si n es menor de 1, el ciclo sigue siendo legal pero MATLAB
no ejecuta la instrucción intermedia. Si x no esta definido,
ó si tiene menos de n elementos, entonces un espacio adicional
es localizado automáticamente a x cada vez que sea necesario.
Puedes anidar los ciclos como en
el siguiente ejemplo:
for
i = 1:m
for j = 1:n
A(i, j) = 1/(i+j-1);
end
end
A
La "A" luego del ciclo
muestra en la pantalla el resultado final. Es importante que
para cada for
halla un end.
La forma general de un ciclo for
es:
for
v = expresión
enunciados
end
La expresión
es en general una matriz. Las columnas de la matriz son asignadas
una por una a la variable v y luego las instrucciones
ó enunciados
son ejecutados.
Usualmente la expresión
es algo como m:n,
ó m:i:n,
que es una matriz con solamente una fila y sus columnas son simplemente
escalares.
Ciclos WHILE
El ciclo WHILE
permite a una instrucción,
ó grupo de instrucciones, repetirse un número indefinido
de veces, bajo el control de una condición lógica.
El siguiente ciclo while
halla el primer entero n para el cual n! es un número
de 100 digitos:
n
= 1;
while prod(1:n) < 1.0e100, n
= n+1; end
n
Un cálculo más práctico
ilustrando el ciclo while
es en el cómputo del exponencial de una matriz, llamado
expm(A)
en MATLAB. Una posible definición de la función
exponencial es mediante la serie:
expm(A)
= I + A + A^2/2! + A^3/3! + ...
La idea es sumar todos los términos
necesarios hasta producir un resultado que, en la precisión
finita la de computadora, no cambie aunque más términos
sean añadidos. Para esto procedemos de la forma siguiente:
E
= zeros(size(A));
F = eye(size(A));
k = 1;
while norm(E+F-E, 1) > 0
E = E + F;
F = A*F/k
k = k+1;
end
Aqui A es la matriz dada, E representa
la suma parcial de la serie, F es un término individual
en la serie, y k es el índice de este término.
La forma general de un ciclo while es:
while
expresión
enunciados
end
Los enunciados
son ejecutados repetidamente mientras todos los elementos de la
matriz en la expresión
sean diferentes de cero.
Enunciados IF y BREAK
A continuación se muestra
como un cálculo se puede dividir en tres casos, dependiendo
del signo ó paridad de un entero n:
if
n < 0
A = negative(n)
else if rem(n, 2) == 0
A = even(n)
else
A = odd(n)
end
En el segundo, partiendo de un entero
positivo n, si este es par, se divide entre dos; si es impar,
se multiplica por tres y se le suma uno. ¿Habrá algún
entero para el cual el proceso nunca termine? Aquí se
ilustran los enunciados while
y if,
también se muestra la función input
(en este caso es una
entrada del teclado), y el enunciado break,
que provee salidas abruptas de los ciclos. Veamos:
%
Problema "3n+1" clásico de la teoria de números.
while 1
n = input('Entre n, negativo termina.
');
if n <= 0, break, end
while n > 1
if rem(n, 2) == 0
n = n/2
else
n = 3*n+1
end
end
end
Archivos-M: Comandos y
Funciones
Los archivos de disco que contienen
instrucciones de MATLAB se llaman archivos-M. Esto es así
porque siempre tienen una extención de ".m"
como la última parte de su nombre de archivo.
Un archivo-M consiste de una secuencia
de instrucciones normales de MATLAB, que probablemente incluyen
referencias a otros archivos-M. Un archivo-M se puede llamar
a sí mismo recursivamente. Puedes crear archivos-M utilizando
un editor de texto ó procesador de palabras.
Hay dos tipos de archivos-M: los
de comandos y las funciones. Los archivos de comandos, automatizan
secuencias largas de comandos. Los archivos de funciones, permiten
añadir a MATLAB funciones adicionales expandiendo asi la
capacidad de este programa. Ambos, comandos y funciones,
son archivos ordinarios de texto ASCII.
Archivos de Comandos
Cuando un archivo de comandos
es invocado, MATLAB simplemente ejecuta los comandos encontrados
en dicho archivo. Las instrucciones en un archivo de comando
operan globalmente en los datos en el espacio de trabajo. Los
comandos son utilizados para hacer análisis, resolver
problemas, ó diseñar secuencias largas de comandos
que se conviertan en interactivas. Por ejemplo, suponga que el
archivo fibro.m
contiene los siguientes comandos de MATLAB:
%
An M-file to calculate Fibonacci numbers
f = [1 1]; i = 1;
while f(i) + f(i+1) < 1000
f(i+2) = f(i) + f(i+1);
i = i + 1;
end
plot(f)
Si escribimos fibro
en una ventana de MATLAB seguido de "enter" vemos que
MATLAB calcula los primeros 16 números de Fibonacci, y
luego grafica estos. Luego que la ejecución del archivo
es completada, las variables f y i permanecen en el espacio de
trabajo.
Los programas de demostraciones incluidos
en MATLAB son ejemplos de como usar comandos para hacer tareas
más complicadas. Para utilizar estos escriba demos
en el "prompt" de MATLAB.
Archivos de Funciones
Un archivo-M que contiene la palabra
function
al principio de la primera línea, es un archivo de función.
En una función, a diferencia de un comando,
se deben de pasar los argumentos. Las variables definidas y manipuladas
dentro de la función son locales a esta y no operan globalmente
en el espacio de trabajo. Los archivos de funciones se
utilizan para extender a MATLAB, i.e., crear nuevas funciones
para MATLAB utilizando el lenguaje propio de MATLAB.
El archivo
mean.m en el disco contiene
las instrucciones:
function
y = mean(x)
% Mean average or mean value.
% For vectors, mean(x) returns the
mean value.
% For matrices, mean(x) is a row
vector
% containing the mean value of each
column.
[m, n] = size(x);
if m == 1
m = n;
end
y = sum(x)/m;
(Las lineas que comienzan con "%"
son interpretadas como comentarios por MATLAB). La existencia
de este archivo en el disco duro define una nueva función
en MATLAB llamada mean.
Si z es un vector de los enteros desde 1 a 99, i.e.,
z
= 1:99;
entonces, el valor promedio es encontrado escribiendo
mean(z)
que resultaría en
ans
=
50
Veamos algunos detalles de mean.m:
La primera línea declara el nombre de la función, los argumentos de entrada, y los argumentos de salida. Sin esta línea sería un archivo de comando.
% indica que el resto de la línea es un comentario.
Las primeras líneas documentan el archivo-M y aparecen en la pantalla cuando escribimos help mean.
Las variables m, n, y y son locales a mean y no existen en el espacio de trabajo. (O si existen, permanecen sin cambios.)
No es necesario asignar los enteros
de 1 al 99 en la variable x. Utilizamos mean
con una variable llamada z. Este vector que contenía los
enteros de 1 a 99 fue pasado ó copiado a mean
donde se convirtió en una variable local llamada x.
Como mejorar la Rapidez
y uso de Memoria de los Programas
Para que los programas en MATLAB
ejecuten más rápido, debemos vectorizar estos
siempre que sea posible. Esto es, debemos convertir los ciclos
for
y while
a operaciones de vectores ó de matrices. Por ejemplo,
un modo de calcular la función "sin" para 1001
números entre 1 y 10 es:
i
= 0;
for t = 0:.01:10
i = i + 1;
y(i) = sin(t);
end
Una versión vectorizada del
mismo código es
t
= 0:.01:10;
y = sin(t);
En una computadora lenta, el primer
ejemplo tomó 15 segundos, mientras que el segundo tomó
0.6 segundos.
Vectores Pre-Asignados
Si no podemos vectorizar un pedazo
de código, podemos hacer que los ciclos for
vayan más rápido pre-asignando cualquier vector
en el cual el resultado de salida sea guardado. Veamos un
ejemplo:
y
= zeros (1,100);
for i = 1:100
y(i) = det(X^i);
end
Si no pre-asignamos el vector "y",
el interpretador de MATLAB irá aumentando el tamaño
de "y" por uno cada vez que se itera en el ciclo.
Archivos de Disco
Manipulación de
Archivos de Disco
Algunos comandos utilizados para
la manipulación de archivos de disco son dir,
type,
delete y
cd. Si la extención
no se especifica, MATLAB utiliza .m
automáticamente. El comando diary
crea un diario de tu sesión de MATLAB en un archivo de
disco. Para más información utiliza la Guía
de Referencia de MATLAB ó el comando help.
Ejecutando Programas Externos
El simbolo
"!" le indica a
MATLAB que el resto de la línea de entrada es un comando
para el sistema operativo. Por ejemplo,
!
edt darwin.m
invoca un editor llamado edt
en un archivo llamado darwin.m.
Luego que este programa sea completado, el sistema operativo
devuelve el control a MATLAB.
Importando y Exportando
Datos
Puedes introducir datos de otros programas a MATLAB por varios métodos. Similarmente, puedes exportar datos de MATLAB a otros programas. También puedes hacer que tus programas manipulen datos directamente en archivos-MAT, el cúal es el formato de archivo utilizado por MATLAB. Para información acerca de las técnicas utilizadas para importar y exportar datos consulte la sección de Importando y Exportando Datos de la guía de MATLAB ó utilice al comando help de MATLAB.
