Capitulo 1

Conceptos Básicos de Análisis Matemático

En este capitulo repasaremos algunos de los conceptos más importantes del cálculo que son esenciales en el estudio de métodos numéricos. Además discutiremos el resultado más fundamental para aproximar funciones ó para hacer estimados de errores: el Teorema de Taylor. Veremos también otros resultados importantes como los Teoremas del Valor Medio para funciones e integrales, el Teorema del valor intermedio, y el Teorema de la funcion implicita.

Resultados Básicos 

El primer resultado básico es el Teorema del Valor Medio para funciones. En palabras y en el contexto físico del movimiento de una particula, este teorema dice que en cualquier intervalo finito de tiempo, la velocidad promedio de la particula en el intervalo es igual a la velocidad instatanea en algún instante de tiempo. Tenemos pues:

Teorema (1.1): (Teorema del Valor Medio para funciones) Sea continua y diferenciable en (a,b) donde a,b son finitos. Entonces existe un número c en (a,b) tal que 

(1.1)

Para intergrales tenemos también un resultado parecido.

Teorema (1.2): (Teorema del Valor Medio para Integrales) Suponga que f y g son funciones continuas en el intervalo acotado [a,b] y que g(x) ³ 0 para toda x en [a,b]. Entonces existe un punto c en [a,b] tal que

(1.2)

En el caso de que g=1, el resultado se puede interpretar como que el area bajo la curva f(x) en el intervalo [a,b] es igual al area del rectangulo con base [a,b] y altura f(c). 

El proximo teorema establece la idea intuitiva de que si una función continua cambia de signo en un intervalo [a,b] entonces en algún punto del intervalo cruzó el eje de x. Veamos: 

Teorema (1.3): (Teorema del Valor Intermedio) Suponga que es continua y que C es un número estrictamente entre f(a) y f(b). Entonces existe un número c en (a,b) tal que f(c)=C. En particular si f(a)f(b) < 0, entonces existe un c en (a,b) tal que f(c)=0.

El siguiente resultado nos provee de condiciones suficientes que garantizan que una ecuación nolineal como f(x,y)=0 se pueda resolver digamos para "x" en terminos de "y".

Teorema (1.4): (Teorema de la Función Implicita): Sea un conjunto abierto, continua y con derivadas parciales continuas en D. Suponga que (x0,y0) en un punto en D tal que

(1.3)

Entonces existe un número y una función continua y con derivada continua tal que

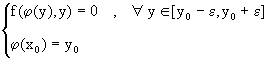(1.4) 

El teorema dice que dadas las condiciones (1.3) podemos resolver la ecuación f(x,y)=0 para "x" en terminos de "y", i.e, , en un intervalo alrededor de y0. Si en (1.3) cambiamos a , entonces podemos resolver para "y" en terminos de "x". En el caso lineal f(x,y)=ax+by+c, el teorema lo que dice es que si a ¹ 0, entonces en f(x,y)=0 podemos despejar para "x" en terminos de "y" lo cúal en este caso es obvio.

Teorema de Taylor 

Un problema común es el de evaluar una función f(x) en un argumento x=a dado. Aunque esto parece un problema sencillo, la función f podria ser desconocida ó complicada para evaluar. Lo que buscamos pues es aproximar a f con una función g que sea más "fácil" de evaluar que f. Los polinomios de Taylor son una forma de hacer esto aunque veremos otras alternativas más adelante.

Polinomio de Taylor de grado uno: Suponga que conocemos f(a) y f '(a). Queremos hallar un polinomio p1(x) tal que p1(a)=f(a), p'1(a)=f '(a). Sabemos que p1(x)=a1+a2x (¿por qué?) de modo que:

 

de donde obtenemos que p1(x)=f(a)+f '(a)(x-a) lo que se conoce como el polinomio de Taylor de grado uno para f en x=a. 

Polinomio de Taylor de grado dos: De igual forma, si conocemos f(a), f '(a), f "(a) podemos construir un polinomio de grado dos p2(x) tal que p2(a)=f(a), p'2(a)=f '(a), p"2(a)=f "(a). Trabajando como arriba obtenemos que 

p2(x)=f(a)+f '(a)(x-a)+(1/2)(x-a)2f "(a) 

lo que se conoce como el polinomio de Taylor de grado dos para f en x=a.

En general si f(a), f '(a),…,f (n)(a) son conocidas, se puede demostrar que el polinomio de grado a lo más n que cumple con las condiciones esta dado por

 

lo que se conoce como el polinomio de Taylor de grado a lo más n para f en x=a. Recuerde aqui que j! denota el factorial de j y se define en forma recursiva por:

 

Ejemplo 1: Considere la función f(x)=1/(1+x) y tomemos a=0. Entonces f '(x)=-(1+x)-2, f "(x)=2(1+x)-3, f(3)(x)=-(2)(3)(1+x)-4, de donde podemos concluir en forma inductiva que

 

Tenemos ahora que

 

En particular

 

Podemos ahora graficar p1, p2, y f en el mismos sistema de coordenadas con las siguientes instrucciones en MATLAB: 

x=linspace(-0.5,0.5,100);
p1=1-x;
p2=p1+x.^2;
f=1./(1+x);
plot(x,p1,x,p2,x,f)
xlabel('X');ylabel('Y');
title('Funcion f(x)=1/(1+x) con sus polinomios de Taylor de grados uno y dos')
text(-0.4,1.8,'f');
text(-0.45,1.4,'p1');
text(-0.45,1.7,'p2'); 

Esto produce la gráfica que se muestra a continuación:

[Image]

Note que el polinomio de grado dos aproxima mejor a f en el intervalo en cuestión pero la diferencia entre los polinomios y la función f (el error) aumenta según nos alejamos del centro a=0.

Queremos ahora de alguna forma cuantificar las observaciones del ejemplo anterior en cuanto al error de aproximación de los polinomios de Taylor. Tenemos pues:

Teorema (1.5) (de Taylor): Suponga que y sea . Sea Rn(x)=f(x)-pn(x) el error en aproximar f con pn. Entonces

 

donde cx es un número entre a y x.

Ejemplo 2: Considere la función f(x)=e2x y tomamos nuevamente a=0. Aqui f(j)(x)=2je2x para toda j³0. Asi que

 

El error de aproximación esta dado por

 

donde cx esta entre cero y x. El caso especial x = ½ nos provee de una fórmula para aproximar el número "e":

Note que

 

donde usamos que como c esta entre cero y ½, entonces ec < e < 3. Si queremos aproximar "e" con la fórmula de arriba con un error (absoluto) de 10-t entonces podemos estimar "n" mediante el siguiente programa en MATLAB:

t=6;
n=0;
R=3;
tol=10^(-t);
while R>tol
n=n+1;
R=3/gamma(n+1);
end
n 

lo cual produce el siguiente resultado para t=6 de n = 10.

Ejemplo 3: Vamos a aproximar la función sen(x) en el intervalo con un error de 10-4. Sabemos que f'(x)=cos(x), f ''(x)=-sen(x), f '''(x)=-cos(x), etc. Tomando a=0 obtenemos pues que f '(0)=1, f ''(0)=0, f '''(0)=-1, etc., de donde podemos concluir que 

 

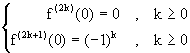
Ahora

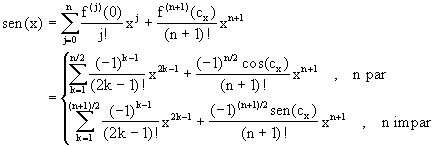
donde cx esta en . Note que en cualquier caso, "n" par ó impar, para el error satisface:

 

Podemos calcular la "n" que hace el error menor de 10-4 mediante el siguiente programa en MATLAB:

t=4;
n=0;
R=pi/2;
tol=10^(-t);
while R>tol
n=n+1;
R=(pi/2)^n/gamma(n+1);
end
n 

lo cual produce el valor de n=10.

En ocasiones podemos calcular polinomios de Taylor de funciones complicadas definidas en terminos de otras funciones para las cuales conocemos sus polinomios de Taylor. Antes de ver un ejemplo de esto, veamos la fórmula para la serie geométrica:

 

Esta fórmula se demuestra facilmente por inducción y en el caso tenemos que

Ejemplo 4: Vamos a calcular un polinomio de Taylor con su residuo para la función log(1+x2). Primero observamos que para t > -1

 

Usando la fórmula de arriba podemos escribir

 

De modo que

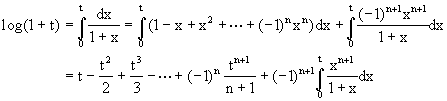
Sustituyendo ahora t=x2 obtenemos

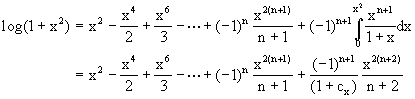
donde usamos el Teorema del Valor Medio para integrales y cx es un número entre cero y x2. Esta fórmula nos da un polinomio para aproximar log(1+x2) con la correspondiente fórmula del error.

Evaluación de Polinomios

Considere el polinomio

p(x)=2 - 3x + 4x2 - 5x3 + 7x4 + 2x5 

Podemos evaluar este polinomio de tres maneras:

  1. Calculamos 2x5, 7x4, -5x3, 4x2, 3x y luego sumamos los resultados. Esto requiere de 5+4+3+2+1=15 multiplicaciones.
  2. Calculamos x2, x(x2)=x3, x(x3), etc. Luego multiplicamos por los coeficientes y sumamos. Esto requiere 4+5=9 multiplicaciones.
  3. Escribimos p(x)=2+x(-3+x(4+x(-5+x(7+2x)))) lo cúal requiere de 5 multiplicaciones.

La tercera forma de evaluar el polinomio es lo que se conoce como el Método de Horner y corresponde exactamente al proceso de evaluación sintética que aprendimos en precálculo. En general para evaluar el polinomio p(x)=a0 + a1x + a2x2 + … + anxn tenemos 

Método

Número de Multiplicaciones

1

n(n+1)/2

2

2n-1

Horner

n

Examinamos ahora en más detalles el método de Horner. Este se método se puede describir por las siguientes iteraciones: dado un número z 

  1. bn = an
  2. Para i=n-1,…,0
  3. bi=ai + z bi+1

Tenemos pues que p(z) = b0. 

Demostración: Por inducción en "n" el grado del polinomio.

(Paso básico) Para n=1, p(x) = a0 + a1x, b1 = a1, b0 = a0 + z b1 = a0 + z a1 = p(z) lo cúal demuestra que el resultado es cierto para n=1.

(Paso inductivo) Vamos a suponer que el resultado es cierto para cualquier polinomio de grado k³1. Entonces para p(x)=a0 + a1x + a2x2 + … + ak+1xk+1 definimos

  1. bk+1 = ak+1
  2. Para i=k,…,0
  3. bi=ai + z bi+1

Defina el polinomio q(x) de grado k por: q(x)=a0 + a1x + a2x2 + … + (ak + ak+1z)xk y los correspondientes b's por:

  2. Para i=k-1,…,0

Observe que p(z)=q(z) y que para 0 £ i £ k. Como el grado de q(x) es k, tenemos por la hipotesis de inducción que . Pero y el resultado es cierto para polinomios de grado k+1 también.

El resultado queda pues establecido para cualquier n ³1. 

El método de Horner lo podemos implementar en MATLAB en forma eficiente. Aqui el arreglo a(1:n) contiene los coeficientes a0, a1, etc. del polinomio. El arreglo "z" puede contener más de un valor de modo que la función evalua el polinomio en el conjunto de datos dados por z:

function pval=hornerV(a,z)
n=length(a); m=length(z);
pval=a(n)*ones(m,1);
for k=n-1:-1:1
pval=a(k)+z.*pval;
end

Ejemplo 5: Para trazar el polinomio p(x)=2 - 3x + 4x2 - 5x3 + 7x4 + 2x5 en el intervalo de [-1,1] podemos escribir:

a=[2 -3 4 -5 7 2];
z=linspace(-1,1,100)';
y=hornerV(a,z);
plot(z,y)
xlabel('x');ylabel('y');
title('p(x)=2-3*x+4*x^2-5*x^3+7*x^4+2*x^5')

lo cual produce la gráfica:

[Image]

Ejercicios

  1. Considere la función en el intervalo [-1,1].
    1. Calcule las formulas de ,i.e., los primeros cuatro polinomios de Taylor de alrededor de .
    2. Grafíque en el mismo sistema de coordenadas los cuatro polinomios.
    3. Estíme gráficamente el error para .
    4. Compare los resultados de la parte (c) con los predichos por la cota del Teorema de Taylor.