Capítulo 2

Representación de Números en la Computadora

En este capítulo estudiaremos como se representan los números en la computadora. Por limitaciones fisicas, los números solo se pueden representar con un número finito de cifras en la computadora. Al igual las operaciones aritméticas que se efectuan en la computadora no corresponden a las operaciones matemáticas exactas. Veremos pues como estas limitaciones en la representación de los números y las operaciones ariméticas afectan los computos y la propagación de errores.

Bases Numéricas y Cambios de Bases

Veamos primero las distintas formas de representar números en terminos de bases distintas. Por ejemplo el número 231.12 base dies se interpreta como: 

(231.12)₁₀ = 2 x 10² + 3 x 10¹ + 1 x 10⁰ + 1 x 10^-1 + 2 x 10^-2 

Otro ejemplo seria:

(101.11)₂ = 1 x 2² + 0 x 2¹ + 1 x 2⁰ + 1 x 2^-1 + 1 x 2^-2 = 4 + 1 + ½ + ¼ = (5.75)₁₀ 

Un ejemplo menos trivial es el siguiente:

donde usamos que

Hemos visto aqui como convertir un número binario a su decimal correspondiente. Veamos ahora como convertimos de decimal a binario. Mostramos aqui el procedimiento convirtiendo (217.732)₁₀ a binario. Trabajamos primero con la parte entera del número. Dividimos esta sucesivamente por dos y llevamos registro de los residuos sucesivos hasta que el cociente sea cero. Estos reciduos desde el último hasta el primero, forman la representación binaria de la parte entera. Veamos

Asi que (217)₁₀=(11011001)₂. Para la parte fraccional, multiplicamos sucesivamente por dos y llevamos cuenta cada ves que el resultado sea mayor de uno ó no. Veamos

En este caso el proceso sigue indefinidamente y escribimos (0.732)₁₀=(0.10111…)₂. Combinando los dos cálculos tenemos (217.732)₁₀=(11011001.10111…)₂.

En los números hexadecimales o base 16 los digitos son

{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}

Aqui (A)₁₆=(10)₁₀, (B)₁₆=(11)₁₀, etc. Por ejemplo

(CD.B9)₁₆=(12 x 16¹ + 13 x 16⁰ + 11 x 16^-1 + 9 x 16^-2)₁₀ 

Los métodos para cambiar de binario a hexadecimal y viceversa son extremadamente sencillos. Historicamente las bases binaria, hexadecimal, y octal han sido las más utilizadas para representar números en la computadora. Esto es básicamente por que el circuito electrico más básico se puede representar por uno si hay corriente ó cero si no hay corriente. Lo que lleva naturalmente al sistema binario como forma de representar el estado del circuito. Esto con lo relativamente fácil de pasar de una base a otra hace que las bases binaria, hexadecimal, y octal sean utilizadas eficientemente para diseñar computadoras.

Números de Punto Flotante

Sea "x" un número real base dies ó dos. Podemos representar a "x" en forma única como sigue:

(2.1) 

donde , "e" es un entero positivo ó negativo, , y es dies ó dos. Por ejemplo

(-117.32)₁₀ = -(0.11732)₁₀ x 10³ , (1101.11)₂ = (0.110111)₂ x 2⁴

La representación de punto flotante del número "x" se denota por fl(x) y consiste de (2.1) con alguna restricción en el número de cifras en y el tamaño de "e". Tenemos pues que

(2.2) 

donde N,M son positivos y , . Los a_i's se obtienen de alguna forma a partir de . El número se conoce como la mantisa y "t" el número de cifras o largo de mantisa. Si alguna operación aritmética produce un resultado con e > M decimos que hubo un overflow. Por el contrario si en el resultado, e < -N decimos que hubo un underflow.

Se puede verificar que "t" cifras en la mantisa equivalen aproximadamente a "t" cifras significativas en la misma base. Ademas "t" digitos binarios equivalen a "t log₁₀2" digitos base dies. 

Veamos ahora varias cantidades importantes del sistema (2.2):

• el número más grande en el sistema es:

  

• el número más pequeño es:

  

• el número positivo "u" más pequeño tal que , llamado el epsilon de la máquina es (¿por qué?)

La dos formas más comunes de calcular la mantisa son:

• Truncación: si entonces . Esto es truncamos a "t" digitos
• Redondeo: en el caso , tenemos

  

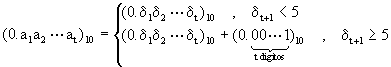
  con las reglas correspondientes base dos.

Tenemos ahora el teorema que nos habla sobre el error en estas dos reglas:

Teorema (2.1): donde

Note que el error en redondeo es en general la mitad del error en truncación. También se puede verificar que como los errores en redondeo varian en signo, estadisticamente "en promedio" tienden a cancelarce. Esta cancelación no es tan probable con truncación. A pesar de estas ventajas la truncación es usada comunmente en el diseño de computadoras por lo fácil de su implementacion a nivel de "hardware".

Estandar de Aritmética de Punto Flotante de la IEEE 

La gran mayoria de las computadoras construidas en los últimos quince años utilizan lo que se conoce como el estandar de aritmética de punto flotante de la IEEE. Esto uniformizó los procesos de representación de números en computadoras distintas facilitando asi las comparaciones y análisis de errores. En este estandar y el flotante de un número tiene la forma: 

(2.3)

donde "f" es ahora la mantisa y satisface y se representa con t cifras binarias. Los valores usados para t y e son como sigue:
 

• en presición sencilla, fl(x) se almacena en una palabra de 32 bits con un bit para , ocho para "e", t = 24, y N = 126, M = 127.
• en presición doble, fl(x) se almacena en una palabra de 64 bits con un bit para , once para "e", t = 52, y N = 1022, M = 1023.

La presición sencilla economiza memoria pero no es mucho más rapida que la presición doble en las computadoras modernas. La distribución de los números de punto flotante en la recta numérica es una nouniforme. De hecho para un exponente "e" dado, los números de punto flotante entre 2^e y 2^e+1 estan uniformemente distribuidos con incremento 2^e-t. Ilustramos esto aqui para el estandar de la IEEE con un sistema trivial donde f y e tienen dos y tres digitos binarios respectivamente. Los números de punto flotante de este sistema los podemos enumerar en la siguiente tabla:

Si ordenamos estos números en forma ascendente obtenemos:

Podemos observar aqui que la densidad de los números de punto flotante disminuye con su tamaño. Podemos también observar esto gráficamente en la siguiente figura:

El número positivo más grande en el estandar de la IEEE esta dado por:

Este número se denota en MATLAB por realmax. Cualquier resultado numérico que produsca un número mayor que realmax se conoce como un overflow y se denota por Inf (infinito) y se representa en (2.3) tomando f=0 y e=1024 en presición doble. El número Inf satisface las relaciones 1/Inf=0 y Inf+Inf=Inf.

El correspondiente número positivo más pequeño es: 

y se denota en MATLAB por realmin. Cualquier resultado numérico que produsca un número menor que realmin se conoce como un underflow y en muchas computadoras el resultado se iguala a cero pero esto no es estandar. Calculos como 0/0, Inf-Inf que pueden conllevar a resultados indefinidos se denotan por NaN (not a number).

El epsilon de la máquina esta dado en este sistema por 2^-t y se denota en MATLAB por eps. Este número corresponde al incremente de los números entre 1 y 2 en el sistema de punto flotante. eps corresponde al error relativo (ver definición más adelante) minimo posible en cualquier computo numérico en el sistema de punto flotante. Toda operación aritmética en la computadora o la representación de punto flotante de un número, induce un error relativo no mayor de eps.

En la siguiente tabla ilustramos estas cantidades especiales con sus respectivas representaciones binarias en la computadora en presición doble:

Propagación de Errores - Perdida de Cifras Significativas 

Como vimos antes, el uso de un número finito de cifras en la representación de punto flotante introduce errores de representación. Aún cuando los números en cuestión se puedan representar en forma exacta en la computadora, estos podrián contener error, por ejemplo si son datos experimentales. Queremos ver como estos errores en los datos se propagan al usar las operaciones aritméticas usuales o más general al evaluar funciones.

Denotamos por x_t el valor real o exacto de una cierta cantidad y x_a una aproximación de x_t obtenida experimentalmente ó al truncar x_t para representarlo en la computadora. Definimos los errores absolutos y relativos respectivamente en x_a como aproximación de x_t por:

Error(x_a) = x_t - x_a , Rel(x_a) = Error(x_a)/x_t 

Se puede demostrar que si , entonces x_a tiene por lo menos m cifras significativas como aproximación de x_t.

Ejemplo 1: Si tomamos x_t=exp(1) y x_a=2.718, tenemos que Error(x_a)=2.8183e-004 y Rel(x_a)=1.0368e-004. 

Uno de los ejemplos más comunes de la propagación de errores es en el fenomeno conocido como perdida de cifras significativas. Este tipo de situación se da cuando algún cálculo numérico envuelve la resta de dos cantidades similares ó en el cálculo de un número por medio de una sumatoria donde el resultado es mucho menor que los terminos de la sumatoria los cuales alternan en signo. Veamos algunos ejemplos:

Ejemplo 2: Considere el cálculo de la función para "x" grande. Suponemos que trabajamos con seis cifras significativas. Veamos el caso de calcular f(100). Note que correctos a seis cifras. Ahora calculamos . El valor exacto a seis cifras de f(100) es de modo que perdimos tres cifras en el computo. ¿Cúal fué el problema? ¡Restamos cantidades similares! En este caso podemos evitar restar cantidades similares si rescribimos f (x) (racionalizando) como: 

Podemos ahora calcular f (100) mediante:

que es correcto a seis cifras. Una situación similar ocurre al usar la fórmula cuadrática. En particular considere la ecuación x²+bx+c/4=0 donde b>0 y c es mucho más pequeño que b. Entonces como el discriminante , vamos a tener cancelación de cifras al calcular la raiz con el "+" en la fórmula cuadrática. Aqui nuevamente una racionalización de la fórmula problemática resuelve el asunto. Si b<0, la raiz problemática es la del "-".

Ejemplo 3: Considere el problema de evaluar

para "x" cerca de cero. Como para "x" cerca de cero, tenemos resta de cantidades similares y por consiguiente habrá perdida de cifras significativas. Ilustramos aqui el uso de polinomios de Taylor para obtener representaciones ó aproximaciones de la función que no conlleven perdida de cifras significativas. Por el Teorema de Taylor tenemos que:

donde esta entre 0 y x. Tenemos ahora que

Note que si , entonces

Podemos pues aproximar a f(x) mediante 

con un error absoluto del orden de 10^-11 y no hay perdida de cifras significativas al calcular con la fórmula aproximada.

Ejemplo 4: Otro caso común de cancelación de cifras significativas ocurre en el cálculo de un número mediante una sumatoria donde los terminos de la sumatoria son mucho mayores que el resultado y alternan en signo. Considere el problema de evaluar el polinomio f(x) = x⁷-7x⁶+21x⁵-35x⁴+35x³-21x²+7x-1. El siguiente código en MATLAB evalua el polinomio en el intervalo [0.988,1.012] y lo grafica:

x=linspace(0.988,1.012,100);
y=x.^7-7*x.^6+21*x.^5-35*x.^4+35*x.^3-21*x.^2+7*x-1;
plot(x,y)

Lo que deberia ser una gráfica suave de un polinomio aparece altamente oscilatoria y de caracter aparentemente aleatorio. Esto se debe a la cancelación severa de cifras significativas en el cálculo donde el resultado final es aproximadamente cero y se toman sumas y diferencias de números del tamaño de . El polinomio de este ejemplo corresponde a la forma expandida de (x-1)⁷ donde graficamos cerca de x=1. Si cálculamos con la fórmula sin expandir no ocurre el problema de cancelación de cifras pero claro lo importante aqui es ilustrar el fenómeno.

Propagación de Errores - Evaluación de Funciones

En los ejemplos anteriores la perdida de cifras significativas se debe primordialmente al uso de un número finito de cifras en los cálculos numéricos. Queremos estudiar ahora el otro aspecto, esto es, suponiendo que se hace uso de un número infinito de cifras en los cálculos, ¿cómo la función ó fórmula que se usa propaga los errores en los datos iniciales? Estudiaremos esto para funciones de una y dos variables.

Suponga que queremos evaluar una cierta función f (x) en un argumento cuyo valor exacto es x_t. Suponga que x_a es una aproximación de x_t. ¿Cómo comparan f(x_t) y f(x_a)? Note que implicitamente asumimos que f se puede calcular exactamente dado un argumento y lo que nos interesa es determinar como f propaga el error en x_a como aproximación de x_t. Usando el Teorema del Valor Medio (cf. Xxx) podemos escribir

para algún c entre x_a y x_t. Dividiendo por f(xt) en ambos lados podemos obtener la siguiente fórmula para los errores relatívos:

Esta fómula nos indica que el número 

actua como un factor de magnificación para el error relativo en x_a. K se denomina como el número de condición. Si suponemos que el error absoluto en x_a como aproximación de x_t es pequeño, podemos aproximar c y x_t por x_a y tenemos que 

(2.4)

Ejemplo 5: Suponga que y que x_a=0.0025 con un error relatívo de 10^-4. Entonces es una aproximación del valor exacto f(x_t) con un error relativo de

En este ejemplo hay que tener cuidado porque la aproximación (2.4) del factor de magnificación K, deteriora según nos acercamos a cero.

Si f es una función de dos variables (x,y), entonces el Teorema del Valor Medio nos dice que si f tiene derivadas parciales continuas, existen c y d tal que

el cúal se puede usar para estimar el error al evaluar f en un argumento aproximado.

Ejemplo 6: Queremos cálcular la distancia focal f de un lente usando la fórmula

donde y . Aqui x_a=32, y_a=46 con errores absolutos de ±1mm. Tenemos pues que

correcto a seis cifras. Este cálculo tiene un error absoluto aproximado de

Ahora obtenemos f tomando el reciproco del resultado de arriba para obtener

que tiene un error absoluto aproximado de

Propagación de Errores en las Funciones Aritméticas

Vamos a considerar ahora los efectos en la propagación de errores en las funciones aritméticas de la computadora. Esto es consideramos ambas fuentes de error: el uso de un número finito de cifras en los cálculos y como la función en si propaga los errores en los datos. 

Las funciones aritméticas son funciones de dos variables de modo que denotamos por x_a y y_a aproximaciones de los valores exactos x_t y y_t. Denotamos por cualquiera de las operaciones y por la operación aritmética correspondiente según se cálcula en la computadora. Vamos a suponer que corresponde a la operación exacta pero truncada a la presición de la máquina. Esto es

(2.5)

Queremos estimar el error 

Pero podemos escribir

(2.6) 

Los dos terminos de la derecha de esta ecuación corresponden a el error propagado por la operación exacta debido a los errores en x_a y y_a, mientras que el segundo termino corresponde a el error causado por el uso de la operación aproximada . Por el Teorema (2.1) y la hipotesis (2.5) tenemos que 

donde esta acotado por el epsilon de la máquina. De aqui que

De aqui que de modo que el termino del error en (2.6) por la operación aritmética aproximada de la computadora es del orden del epsilon de la máquina. El termino del error propagado en (2.6) es pues el más significativo y su comportamiento depende de la operación aritmética en cuestión. Veamos el caso en que . Escribimos en lugar de . Escribimos 

Entonces el error propagado se puede expresar como

el cual se puede estimar con los estimados de y los valores de x_a, y_a. Podemos más aún calcular el error relativo en x_ay_a como sigue:

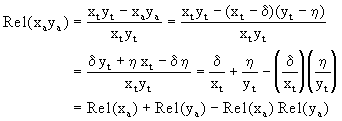
de donde tenemos que si Rel(x_a) y Rel(y_a) son pequeños, entonces Rel(x_ay_a) será pequeño y se puede aproximar por

Decimos pues que la multiplicación es una operación estable. En forma similar se demuestra que

obteniendo asi que la división es también una operación estable. Para la suma y la resta la situación es distinta. Es fácil ver que

que es pequeño dado que lo son. Pero para el error relativo tenemos que

el cual puede ser bien grande aunque sean pequeños si . Este es el fenómeno de perdida de cifras significativas que vimos anteriormente.

Sumatorias

En esta sección estudiamos el problema de sumar muchos números en la computadora. Como cada suma introduce un error, proporcional al epsilon de la máquina, queremos ver como estos errores se acumulan durante el proceso. El análisis que presentamos generaliza al problema del cálculo de productos interiores.

El problema es pues cálcular la sumatoria

usando aritmética de punto flotante. Definimos pues

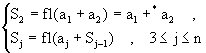
Queremos determinar el error S - S_n. Motivados por el Teorema (2.1) definimos por

donde tomamos S₁=a₁. Tenemos ahora:

Teorema (2.2):

Demostración: Procedemos por inducción en el número de terminos en la sumatoria.

1. Paso básico: Aqui lo cúal concide con la fórmula del teorema.
2. Paso inductivo: Suponemos que el resultado es cierto para n = m, i.e.,

   

   Ahora verificamos que el resultado también es cierto para n = m+1. Pero

   

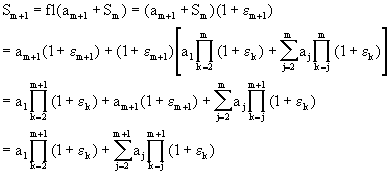
   lo cual es el resultado para n = m+1.

3. Por el Principio de Inducción Matemática, el resultado del teorema es cierto para toda n³2.

Como los e_i's son pequeños, podemos aproximar

Asi que por el resultado del teorema

De aqui que

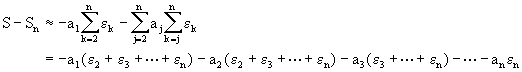
Asi que si queremos minimizar el error en la sumatoria calculada, debemos ordenar los a_i's de modo que

i.e., debemos sumar los núeros más pequeños primero y luego los grandes. Note pues que la suma no es una operación conmutativa en la computadora. 

Un análisis similar pero más complicado matemáticamente se puede hacer para el producto interior

Note que en el análisis de arriba no se tomaron en consideración posibles errores en los datos a_i's. Estos efectos se pueden incluir también en el análisis. (Ver ejercicio (7)).

Ejercicios

1. Suponga que y que calculamos

   

   en el orden de la siguiente figura (para

   

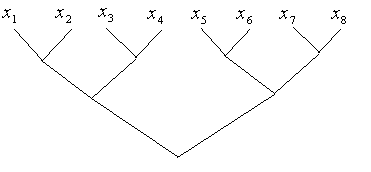
   Obtenga los estimados de los errores "forward" y "backward" para este cómputo.

2. El polinomio se evalúa en un sistema de punto flotante mediante la regla de Horner. Muestre que el valor calculado satisface

   

   donde es el epsilon de la máquina. (Los terminos se pueden descartar).

3. ¿Con cúanta precisión necesitamos conocer a p para poder calcular correcto a cuatro cifras?
4. Trace la gráfica de la función en el intervalo para . Evalúe la función de dos formas:
   • normal:
   • anidada:

   Observe cualquier diferencia o características particulares en las gráficas. Comente.

5. Considere la recurrencia donde . Verfique que la solución exacta de esta recurrencia es:

   

   Resuelva esta recurrencia en la computadora. Haga una gráfica de k vs . Explíque la gráfica.

6. Sean donde . Defina

   

   Suponiendo que y que r £t, calcule el error