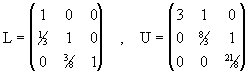Capítulo 3

Sistemas Lineales

Los sistemas de ecuaciones lineales son una de las herramientas matemáticas de modelaje más comunes en las aplicaciones. Una clasificación común de los sistemas lineales es por su tamaño. Los sistemas con O(100) variables se consideran pequeños y usualmente se utilizan los llamados métodos directos para su solución. Los sistemas de O(1000) ó más variables se consideran grandes o de gran escala y los métodos de solución más eficientes por lo general son los llamados métodos iterativos o indirectos. Otra clasificación importante de los sistemas lineales es por la cantidad o densidad de ceros de la matriz de coeficientes. Los sistemas con pocas entradas distintas de cero se llaman escasos. De lo contrario decimos que el sistema es denso. El aprovechar la estructura de ceros de la matriz de coeficientes nos lleva por lo general a algorítmos mucho más eficientes que los convencionales. 

La solución directa de sistemas de ecuaciones lineales conlleva esencialmente dos etapas: transformación del sistema original a otro sistema equivalente más "simple" y luego la solución del nuevo sistema equivalente. La transformación del sistema original a uno más simple toma muchas formas la más común de ellas siendo el proceso de Eliminación Gaussiana. En este método, en su forma básica, si ninguno de los pivotes se hace cero, se producen como resultado matrices L y U triangulares inferior unitaria y superior respectivamente tal que A=LU donde A es la matriz de coeficientes del sistema original. El sistema Ax=b se puede resolver ahora en dos etapas adicionales.

Problema Básico y Notación 

Un sistema lineal de n ecuaciones en n desconocidas se puede escribir de la forma

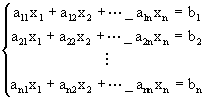(3.1)

donde los son dados y x₁,x₂,…,x_n son desconocidas. Si definimos la matriz A y los vectores b, x por 

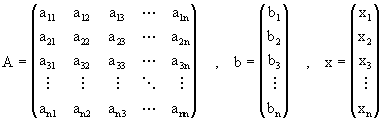(3.2) 

Entonces podemos escribir el sistema (3.1) en forma matricial como Ax=b. La matriz A se conoce como la matriz de coeficientes del sistema y b como el lado derecho. Si b=0, i.e., b_i=0, 1 £ i £ n, entonces decimos que el sistema es homogeneo. De lo contrario se dice que es nohomogeneo.

Ejemplo 1: Considere el sistema

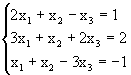
Si definimos

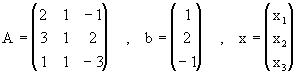
Entonces podemos escribir el sistema en forma matricial como Ax=b.

¿Cúando tiene (3.1) solución y que esta sea única?

Teorema (3.1): Sea A una matriz n ´ n y b un vector. Las siguientes aseveraciones para el sistema Ax=b son todas equivalentes:

1. El sistema tiene solución que es única para todo lado derecho b.
2. El sistema tiene por lo menos una solución para todo lado derecho b.
3. El sistema homogeneo asociado tiene x=0 como única solución.
4. det(A) ¹ 0
5. A es invertible

Eliminación Gaussiana

Vamos ahora a estudiar el método más básico y a la ves más importante para la solución directa de sistemas lineales. Primero ilustramos el método con un ejemplo y despúes lo generalizamos.

Ejemplo 2: Considere el sistema de ecuaciones siguiente: 

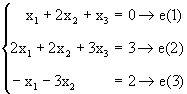
Podemos resolver esto mediante eliminación Gaussisana como sigue:

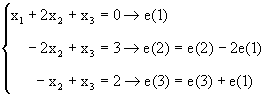
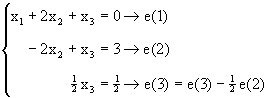
Con este último sistema equivalente podemos obtener la solución sustituyendo para atrás:

Vamos a generalizar este ejemplo a un sistema 3´3 general. Escribimos el sistema original como

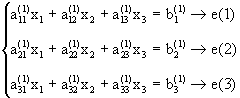(3.3)

Paso 1: Suponemos que y definimos 

se llama el pivote en este paso. El sistema (3.3) reduce ahora a:

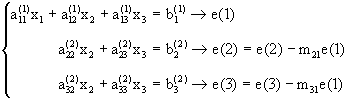(3.4)

donde

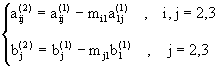
Paso 2: Suponemos ahora que y definimos

Ahora (3.4) reduce a:

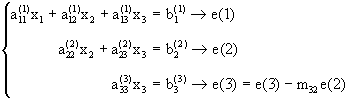
donde

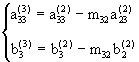
Paso 3: Hacemos ahora la sustitución para atrás para obtener la solución. Suponemos aqui que :

Pasamos ahora al caso general del sistema:

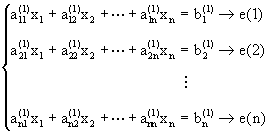
Primero pasamos por la etapa de eliminación. Esto es, para k=1,2,…,n-1:

Paso k: Suponemos que (pivote). El sistema en este paso se reduce a uno de la forma:

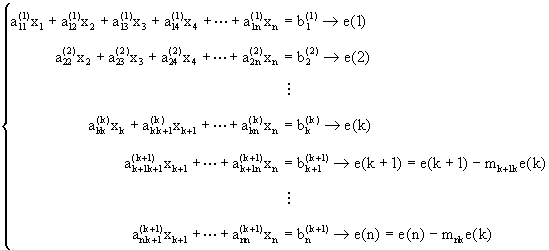
donde

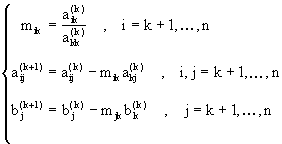(3.5)

En el último paso llegamos a un sistema triangular superior de la forma:

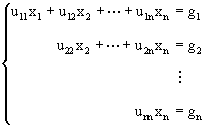(3.6)

donde

(3.7)

Paso n: Calculamos finalmente la solución del sistema haciendo sustitución para atrás:

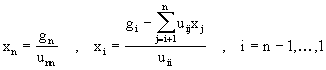(3.8)

Las fórmulas (3.5), (3.7), (3.8) definen el Método de Eliminación Gaussiana en su forma básica. Las formulas (3.5) definen la parte de eliminación del método mientras que (3.8) nos da la sustitución para atrás.

Antes de entrar en las variantes de el método básico vamos a hacer un estudio de la cantidad de operaciones envueltas en el método. Esto se conoce como un conteo operacional. Examinando las fórmulas para los en (3.5) podemos construir la tabla siguiente:

donde usamos las fórmulas 

Es costumbre contar las operaciones de multiplicación y división juntas. De modo que la tabla de arriba la podemos resumir diciendo que en la parte de eliminación del método de eliminación Gaussiana el total de:

Sumas y Restas =

Multiplicaciones y Divisiones =

Las fórmulas para los en (3.5) se conocen como la modificación del lado derecho. Estas conllevan:

Sumas y Restas = n-1 + (n-2) + … + 1 =

Multiplicaciones y Divisiones = n-1 + (n-2) + … + 1 =

Las fórmulas (3.8) de la sustitución para atrás conllevan los siguientes totales de operaciones:

Sumas y Restas = 1 + 2 + … + (n-1) =

Multiplicaciones y Divisiones = 1 + 2 + … + n = 

Combinando todos los totales parciales hasta ahora obtenemos que el proceso completo de eliminación Gaussiana conlleva un total de:

Sumas y Restas =

Multiplicaciones y Divisiones =

Note que para n "grande" ambos resultados son aproximadamente (1/3)n³. Asi que por ejemplo doblar n equivale a aproximadamente ocho veces más tiempo computacional. Observe también que la parte de eliminación es la que contribuye el termino proporcional a n³. La modificación del lado derecho y la sustitución para atrás son ambas proporcionales a n². Note que estos tres procesos son independientes uno del otro. Por consiguiente si hay la necesidad de resolver varios sistemas todos con la misma matriz de coeficientes, la parte de eliminación debe hacerse una sola ves.

Al derivar las fórmulas (3.5), (3.7), (3.8) asumimos que los pivotes . Si por el contrario algún , entonces podemos argumentar matemáticamente que algún si la matriz de coeficientes del sistema original es nosingular. En tal caso podemos intercambiar la fila "i" con la "k" y continuar el proceso. A pesar de esto un pivote pequeño, aunque distinto de cero, puede causar que los efectos de redondeo debido a la aritmética finita de la computadora se propagen rápidamente.

Ejemplo 3: Considere el sistema

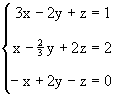
El determinante de la matriz de coeficientes es -20/3 de modo que es nosingular. Vamos a resolver el sistema pero usando solo cuatro cifras decimales. Representamos el sistema con la matriz aumentada:

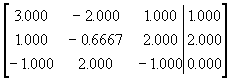
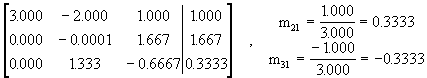
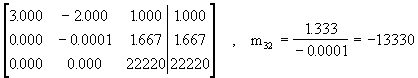
De donde obtenemos que z = 1, y = 0, x = 0.6667. ¡La solución exacta del sistema es x=½, y=¾, z=1!

Para evitar el problema de pivotes distintos de cero pero pequeños usamos lo que se denomina como pivoteo parcial. Esto es, definimos el indice i₀ por:

(3.9)

Si i₀¹k, entonces intercambiaamos las filas i₀ y k. Note que estamos haciendo el pivote máximo en valor absoluto. De esta forma los multiplicadores m_ik satisfacen 

lo cúal es lo que ayuda con la propagación de errores. Existe otra variante del pivoteo. En este caso se determinan los indices i₀ y j₀ tal que:

(3.10)

y se intercambian las filas i₀ y k y las columnas j₀ y k si i₀¹k ó j₀¹k respectivamente. Esto se conoce como pivoteo total y se puede demostrar que es más efectivo que el pivoteo parcial en el control de la propagación de errores. Pero el cálculo del máximo en (3.10) es mucho más costoso que en (3.9) por lo que en la practica se prefiere el pivoteo parcial. Además se ha observado en pruebas usando matrices generadas aleatoriamente, que la diferencia entre ambos métodos no es significativa en terminos de la propagación del error.

Cálculo de la Inversa de una Matriz

Suponga que A es una matriz nosingular y A^-1 su inversa. Escribimos A^-1 y la matriz identidad I en forma particionada como

A^-1 = (x₁,x₂,…,x_n) , I = (e₁,e₂,…,e_n)

donde los e_i's forman la base estandar de . Ahora como A A^-1 = I, tenemos que 

Ax_i = e_i , 1 £ i £ n     (3.11)

Asi que para calcular A^-1 debemos resolver n sistemas distintos pero con la misma matriz de coeficientes A. La eliminación de A la hacemos una ves lo cual requiere (1/3)n³ operaciones aproximadamente. La modificación del lado derecho y la sustitución para atrás de cada uno de los sistemas en (3.11) conlleva aproximadamente n² operaciones cada uno. Asi que en total tenemos (1/3)n³+n(n²) = (4/3)n³ aproximadamente. (Este conteo se puede mejorar a (5/6)n³). En muchas ocaciones las fórmulas que envuelven inversos de matrices se pueden rescribir en terminos de sistemas lineales intermedios. Por el conteo operacional de arriba, las fórmulas con los sistemas lineales son preferibles ya que la solución de cada sistema envuelve aproximadamente (1/3)n³ operaciones mientras que calcular los inversos toma (4/3)n³ operaciones. Como regla general tenemos pues que:

LOS INVERSOS DE MATRICES NO SE CALCULAN A MENOS QUE SE NECESITEN EXPLICITAMENTE. 

Veamos una aplicación de esta regla. Supongamos que desamos calcular la expresión donde c, b son vectores en y A es n´n. Si calculamos A^-1, luego multiplicamos por b y finalmente el producto interior con c tenemos aproximadamente

Si en lugar de esto calculamos a mediante:

• Halle la solución x del sistema Ax=b
• Calcule

un análisis similar al de arriba nos da aproximadamente (1/3)n³+n²+n lo cual es mucho mejor que la fórmula directa.

Factorización LU de una Matriz 

Para discutir la factorización LU de una matriz necesitamos priemro definir dos tipos especiales de matrices. Una matriz A=(a_ij) se dice que es triangular superior si a_ij=0 para toda i > j. A es triangular inferior si a_ij=0 para toda i < j. El adjetivo unitaria se añade en ambos casos si en adición a_ii=1 para toda i. Una matriz que es ambas triangular superior e inferior se llama diagonal. Note que una matriz diagonal satisface a_ij=0 para toda i ¹ j.

Ejemplo 4: Las matrices 

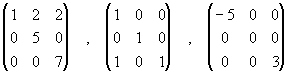
son triangular superior, inferior y diagonal respectivamente. 

La matriz de coeficientes del sistema (3.6) es triangular superior y la denotamos por U=(u_ij). Usando los multiplicadores m_ik en (3.5) podemos definir la matriz triangular inferior unitaria L por:

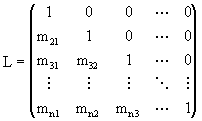
Teorema (3.2): Sea A una matriz n´n nosingular. Defina las matrices L y U como arriba. Entonces si no se hace pivoteo en el proceso de eliminación Gaussiana, tenemos que A=LU.

Demostración: El elemento (i,j) del producto LU consiste del producto interior de la fila i de L con la columna j de U. Esto es

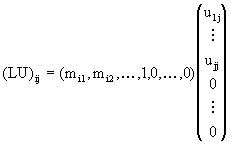
Si i £ j, tenemos que

Usando las fórmulas (3.5) y la definición de U podemos escribir esto como

donde para simplificar la segunda sumatoria usamos que esta es telescópica. Ahora si i > j

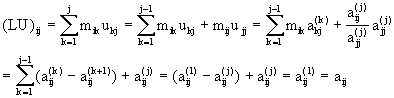
Como (LU)_ij=a_ij para toda i,j tenemos que A=LU.

Ejemplo 5: Para la matriz

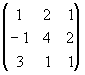
tenemos que mediante eliminición Gaussiana 

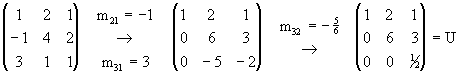
Si definimos ahora

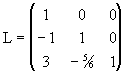
tenemos que A=LU.

Dado que A=LU, el sistema Ax=b se puede escribir como LUx=b. La solución del sistema Ax=b se puede ver entonces en tres etapas: 

1. (Eliminación) Calcular la factorización A=LU.
2. (Modificación del lado derecho) Resolver el sistema triangular inferior Lg=b para el vector g.
3. (Sustitución para atras) Resolver el sistema triangular superior Ux=g para el vector x.

Ejemplo 5: Resuelva el sistema 

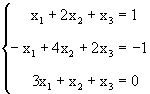
La matriz de coeficientes de este sistema coincide con la del ejemplo anterior de modo que

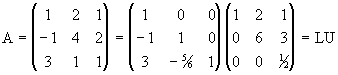
La solución de Lg=b con b=(1,-1,0)^t esta dada por:

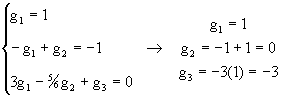
Ahora Ux=g nos da la solución del sistema original:

Variantes del Método de Eliminación Gaussiana 

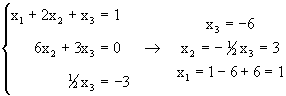
Vamos ahora a discutir dos métodos alternos para calcular la factorización LU de una matriz pero que aprovechan alguna estructura particluar de la matriz. El primero de ellos es la Factorización de Cholesky que se usa para matrices simétricasy positivas definidas. El otro método aprovecha la estructura escasa de la matriz en el caso que esta sea tridiagonal.

Factorización de Cholesky 

Una matriz A es simétrica si A^t=A. Decimos que A es positiva definida si x^tAx>0 para todo x¹0. Se puede demostrar que una matriz simétrica es positiva definida si y solo si todos sus valores propios son positivos. También se puede demostrar que existe una matriz triangular inferior L tal que

A = L L^t

lo cual se conoce como la factorización de Cholesky de A. De hecho las entradas de L=(l_ij) de pueden calcular mediante las fórmulas:

1. Para i=1,2,…,n
   1. 
   2. Para j=1,2,…,i-1                                             (3.12)
      1. 

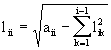
Estas fórmulas se obtienen multiplicando las filas de L por las columnas de L^t e igualando a las entradas correspondientes de A. Un conteo operacional de estas fórmulas muestra que el total de operaciones es aproximadamente (1/6)n³, i.e., la mitad que en eliminación Gaussiana básico. (Note sin embargo que hay que calcular n racies cuadradas). La ganacia aqui se debe a que se utilizó la simetría de la matriz A. Note también que como A es simétrica solo hay que almacenar en la computadora la mitad de la matriz al igual que para L que es triangular inferior.

Sistemas Tridiagonales

Una matriz A se llama tridiagonal si a_ij=0 para toda i,j tal que ½i - j½ > 1. Esto es, todas las entradas de A son cero excepto posiblemente en las diagonales inferior, superior y principal. Podemos pues escribir A de la siguiente forma: 

(3.13)

Para almacenar A en la computadora usamos tres vectores de tamaño n lo que da un total de 3n lugares de memoria en comparación con n² para una matriz densa. Vamos ahora a resolver el sistema Ax=b aprovechando la estructura de ceros de A. Primero buscamos la factorización LU de A. Para esto buscamos L y U de la forma:

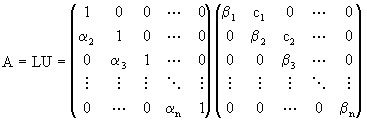(3.14)

Multiplicando e igualando a las entradas correspondientes de A obtenemos: 

• fila uno de L por columna uno de U:
• fila dos de L por columna uno de U:
• fila dos de L por columna dos de U:
• fila tres de L por columna dos de U:
• fila tres de L por columna tres de U: , etc.

De esta forma obtenemos las fórmulas:

1. 
2. Para j=2,3,…n
   1.                                       (3.15)
   2. 

El total de multiplicaciones y divisiones en estas fórmulas es 2n-2 (compare con (1/3)n³ para eliminación Gaussiana básico). Para resolver Lg=b es fácil ver que las fórmulas son: 

1. 
2. Para j=2,3,…,n                                             (3.16)
   1. 

El total de multiplicaciones y divisiones en este cálculo es de n-1. Finalmente la solución de Ux=g se obtinene mediante las fórmulas:

1. 
2. Para j=n-1,n-2,…,1                                     (3.17)
   1. 

El conteo aqui de multiplicaciones y divisiones es de 2n-1. Asi que en total para resolver el sistema Ax=b donde A es tridiagonal se requieren de 5n-4 multiplicaciones y divisiones. En todo este proceso necesitamos que los pivotes y es conveniente que los 's sean menor de uno en valor absoluto. Esto se cumple si

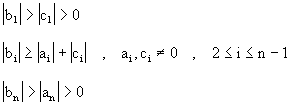       (3.18)

Ejemplo 6: Considere la matriz tridiagonal 

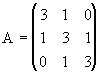
Aqui a_j=1, j=2,3, b_j=3, j=1,2,3, c_j=1, j=1,2. Asi que

de donde obtenemos que