una
aproximación de b y
la solución
del sistema (aproximado)
. Queremos
estimar el error 
en terminos la diferencia
. Para esto
definimos:
En esta sección estudiaremos cúan sensitiva es la solución
del sistema lineal Ax=b a cambios o perturbaciones en los datos A y b. Note
que A ó B pueden contener errores ya sea por las truncaciones envueltas
al entrar estos en la computadora o porque sean datos experimentales. De
modo que queremos ver como esto puede afectar la solución calculada
x. Primero estudiamos variaciones en b unicamente. Sea
una
aproximación de b y
la solución
del sistema (aproximado)
. Queremos
estimar el error
en terminos la diferencia
. Para esto
definimos:
(3.19)
Estas se conocen como la norma vectorial infinita y la norma matricial asociada respectivamente. Estas normas satisfacen las siguientes propiedades para cualesquieras vectores x,y y matrices A,B:
(desigualdad
triangular)
Tenemos ahora el siguiente teorema:
Teorema (3.3): Sea A una matriz nosingular. Sean
x,
las soluciones
de los sistemas Ax=b y
. Entonces
(3.20)
Demostración: De Ax=b y
obtenemos
que 
. Como
A es nosingular, entonces
. Usando la
propiedad (4) de las normas obtenemos que
. Dividiendo
por 
en ambos
lados obtenemos
Pero 
. Usando
esto arriba obtenemos el resultado.
Si definimos 
,
y el número de condición de A por
(3.21)
entonces podemos escribir el resultado del teorema como
(3.22)
De modo que si 
es "grande", entonces
se puede
magnificar por un factor hasta de
. Decimos pues
que el sistema Ax=b es mal acondicionado si
es "grande".
De lo contrario el sistema se dice que es bien acondicionado. Note
que como 
,
entonces
i.e., 
para
toda matriz A. En MATLAB podemos calcular el número de condición
de A con la instrucción cond(A). Este
no es el número de condición en la norma (3.19) pero si en
lo que se conoce como la norma dos de A. La instrucción rcond(A) nos
da una aproximación del inverso de
cond(A). rcond
es mucho más rápida que cond
para matrices de tamaño grande.
En forma similar se puede demostrar el resultado que incluye variaciones en A y b ambas. Simplemente enunciamos el resultado.
Teorema (3.4): Sea A una matriz nosingular y
otra matriz
tal que
(3.23)
Entonces es
nosingular y
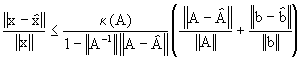(3.24)
Ejemplo 7: La matriz de Hilbert de orden n se define por
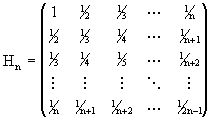(3.25)
Note que Hn es simétrica para toda n ³ 1. Usando la instrucción de MATLAB, hilb(n) podemos generar la matriz de Hilbert de orden n. La instrucción invhilb(n) calcula el inverso exacto de Hn. Por ejemplo
hilb(5)
ans =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
que es la matriz de Hilbert de orden 5 truncada a cuatro cifras aunque MATLAB guarda más cifras internamente. Mientras que
invhilb(5)
ans =
25 -300 1050 -1400 630
-300 4800 -18900 26880 -12600
1050 -18900 79380 -117600 56700
-1400 26880 -117600 179200 -88200
630 -12600 56700 -88200 44100
produce el inverso exacto de H5. Podemos calcular el número de condición de H5 según definido en (3.21) mediante:
norm(hilb(5),inf)*norm(invhilb(5),inf)
ans =
943656
lo que indica el mal acondicionamiento de la matriz de Hilbert apenas para n=5. Este número compara con
cond(hilb(5))
ans =
4.7661e+005
y con
1/rcond(hilb(5))
ans =
6.9409e+005
Usando la instrucción flops de MATLAB podemos estimar que el computo con cond requiere de 937 operaciones de punto flotante mientras que el cálculo con rcond toma 296 operaciones.
El Método de Eliminación Gaussiana produce la solución exacta de un sistema lineal en aproximadamente (1/3)n3 operaciones aritméticas donde n es el orden de la matriz de coeficientes A. En general, debido a que los cómputos se hacen con precisión finita, la solución obtenida por Eliminación Gaussiana no es la solución exacta del sistema (aunque esta cerca de serlo si el sistema es bien acondicionado). Veamos ahora un proceso iteratívo que toma la solución calculada por el Método de Eliminación Gaussiana y trata de mejorarla.
Sea x(0) la solución calculada por Eliminación Gaussiana
y x la solución exacta del sistema, i.e., Ax=b. Para cualquier
defina
(error exacto)
y 
(los residuos).
Entonces es fácil ver que
, de modo que
utilizando la factorización LU de A ya calculada para obtener
x(0), podemos resolver
. Este sistema
tampoco se puede resolver en forma exacta obteniendo asi una aproximación
e(k) de
. Definimos
ahora 
la
cual debe ser una mejor aproximación de x que
. El proceso
continua de esta manera en forma inductiva hasta que un cierto criterio de
"paro" se cumple y el proceso termina. En forma algorítmica
tenemos:
.
.
.
Note que en el cálculo del residuo r(k) en el paso (3a) tenemos cancelación de cifras significativas ya que Ax(k)»b. Para evitar esto el cálculo debe hacerse en presición extendida y el resto de los cálculos en presición normal. El ciclo en (3) se puede detener con un criterio como
(3.26)
lo que garantiza t cifras correctas en la solución calculada en caso de convergencia. Normalmente sin embargo el ciclo no debe ejecutarse más de dos veces.
Note que el cálculo de r(k) en (3a) requiere de n2 multiplicaciones con aproximadamente la misma cantidad de sumas y restas. Para la solución del sistema en (3b) se usa la factorización LU de A del paso (1) de modo que esto toma aproximadamente n2 operaciones. Asi que cada pasada por el ciclo (3) conlleva aproximadamente 2n2 multiplicaciones y divisiones.
Ejemplo 8: Considere el sistema lineal
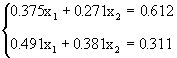
La solución exacta a tres cifras significativas es x1=15.2, x2=-18.7. Si resolvemos el sistema mediante eliminación Gaussiana sin pivoteo y usando aritmética de tres cifras tenemos:
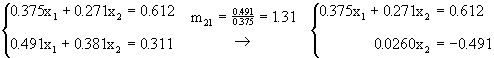
de donde obtenemos
. El residual
de esta solución calculada esta dado por:
correcto a tres cifras. Podemos calcular e(0) mediante:
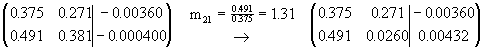
de donde obtenemos que
. La
solución mejorada es:
lo cúal es mejor que x(0). El proceso se puede repetir una o dos veces mas.
Cuando usamos Eliminación Gaussiana para resolver el sistema Ax=b
en una computadora normal, ocurren errores de redondeo en cada paso del proceso
debido a la aritmética finita de la máquina. Queremos estudiar
como estos errores se propagan o acumulan durante todo el proceso y estimar
el error en la solución calculada. En realidad al final del proceso
de eliminación Gaussiana obtenemos un vector
tal que
. En el
análisis de errores hacia atras nos interesa saber si
es la
solución exacta de otro problema que este cerca del problema original
en cierto sentido.
Primero repasamos algunas de las fórmulas del Capítulo 2. En
particular recordamos que las operaciones aritméticas de la computadora
se asumen que corresponden a la operación exacta pero truncada al
número de cifras de la máquina. Esto es si
denota la
operación aritmética
en la computadora,
entonces
(3.27)
donde 
para
el sistema de punto flotante (2.2) y
para el estandar
de la IEEE (2.3). Usando estas fórmulas repetidamente en (3.5), (3.8),
similar al análisis que hicimos de la sumatoria de n numéros,
obtenemos el siguiente resultado.
Teorema (3.5): Sea
la solución
calculada del sistema Ax=b mediante eliminación Gaussiana usando
aritmética de punto flotante base b con
una mantisa de t cifras. Sea u el epsilon de la máquina. Entonces
es la
solución exacta del sistema
donde
H=(hij) y
(3.28)
donde n es el tamaño de A y
(3.29)
El factor 
del teorema mide la razón de crecimiento de las entradas de la matriz
de coeficientes según el método numérico progresa. La
cota superior de este factor depende de la estrategia de pivoteo que se use.
En particular
, para pivoteo
parcial (3.30)
, para pivoteo
completo o total
En cualquiera de los dos casos, si n no es muy grande, el teorema lo que
dice es que
es solución exacta de un problema que esta cerca del original. En
este sentido es que decimos que Eliminación Gaussiana es un método
estable. Esto no implica que
esté
cerca de la solución exacta x. De hecho si tomamos
en el Teorema
(3.4) y usamos las cotas del Teorema (3.5) obtenemos que
(3.31)
lo que dice que
estará cerca de x si A es una matriz bien acondicionada.
Dada una matriz A nxn de entradas complejas, un número
C (conjunto
de los números complejos) es un valor propio de A si existe
un vector 
tal que 
. Usando
propiedades de determinantes, es fácil ver que el problema de hallar
los valores propios de una matriz es equivalente al de hallar las raices
de un polinomio con coeficientes complejos. Por el Teorema Fundamental del
Algebra, tenemos ahora que toda matriz nxn tiene exactamente n valores propios
contando multiplicidades. También tenemos, por un teorema famoso de
Galois, que el cálculo de los valores propios de una matriz no se
puede hacer utilizando unicamente formulas algebraicas. Por tal razón
el cálculo de los valores propios de matrices es un problema
computacionalmente complejo y el poder estimar los mismos es de vitál
importancia. El estimado más crudo de los valores propios de una matriz
esta dado por la desigualdad
, donde
es valor
propio de A} (3.32)
se conoce como el radio espectral de A. Este estimado aunque útil en muchas ocaciones, no es muy preciso en cuanto a la localización de los valores propios de A. El Teorema de Gerschgorin va más allá en este sentido. Para A=(aij) definimos los radios
(3.33)
y los discos
(3.34)
El Teorema de Gerschgorin establece que cada valor propio de A pertenece al menos a uno de los Di’s y que si k de los discos de Gerschgorin se intersecan entre si y estan aislados de los otros discos, entonces su unión contiene exactamente k de los valores propios de A.
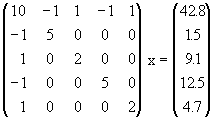
es conveniente intercambiar primero las filas uno y cinco y luego las columnas uno y cinco (¿por qué?). Resuelva el sistema luego de permutar y calcúle la factorización LU de la matríz permutada.
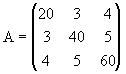
usando aritmética finita con dos cifras decimales. El sistema
donde
tiene la
solución aproximada
. Calcúle
una mejor aproximación mediante un paso de refinamiento iterativo.
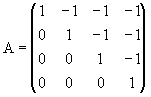, b =
calcule una solución aproximada de Ax=b primero redondeando las entradas
de b al entero más cercano y luego resolviendo el resultante. Verifique
que la solución calculada es
= (12, 4,
2, 1)t. Sea
el vector
residual.
.
A = round(10 * rand(6)) ,
s = ones(6, 1) ,
b= A*s.
La solución al sistema lineal Ax = b es claramente s. Resuelva el sistema utilizando la operación \ de MATLAB. Calcule el error x - s. Ahora perturbamos el sistema como sigue. Deje que
t = 1.0e-12, E = rand(6) - 0.5, r = rand(6, 1) - 0.5
y sean
M = A + t * E, c = b + t * r
Resuelva el nuevo sistema perturbado Mz = c para z. Compare la solución z con la solución del sistema original calculando z - 1. ¿Cómo se compara el tamaño de la perturbación en la solución a el tamaño de las perturbaciones en A y b? Repita el análisis de perturbación con t =1.0e-04 y t =1.0e-02. ¿Es ó no el sistema Ax = b bien acondicionado? Explique. Utilice MATLAB para calcular el número de condición de A.
X = zeros(lenght(t), 5) , Y = X .
Las matrices X y Y se generan utilizando los siguientes comandos de MATLAB:
for i = 1 : 5
X (: , i) = r(i) * cos(t) + real (A (i, i));
Y (: , i) = r(i) * sin(t) + imag (A (i, i));
end
Sea e = eig(A). Podemos ahora graficar los valores propios y los discos de Gerschgorin con el comando
plot(X, Y, real(e), imag(e), 'x') .
B = [3 0.1 2; 0.1 7 2; 2 2 50]
D = diag([0.1, 0.1, 1]) , 
.
La nueva matriz C tiene los mismos valores propios que B. ¿Por qué? Explique. Utilice C para hallar intervalos que contengan los otros dos valores propios de B. Calcule y grafique los discos de Gerschgorin de C.
