Capítulo 4

Solución de Ecuaciones Nolineales 

Suponga que f es una función continua digamos . Deseamos calcular soluciones de la ecuación escalar nolineal

f(x) = 0                  (4.1)

Más general aún, podemos considerear el caso en que donde n³1. Entonces (4.1) representa un sistema de ecuaciones nolineales. Problemas del tipo (4.1) aparecen en la optimización de funciones y en la solución numérica de problemas de frontera nolineales. En este capítulo enfocaremos más en el problema escalar y discutiemos los apectos básicos del caso de sistemas de ecuaciones.

Método de la Bisección

Este método tiene como base ó motivavión el Teorema (1.3), Teorema del Valor Intermedio. En particular, si f es una función continua digamos , y a, b son dados tales que f(a)f(b)£0, entonces definimos c=(a+b)/2. Si f(c)=0, entonces terminamos. De lo contrario remplazamos a ó b con c manteniendo la diferencia en signos, etc. Esto nos lleva al siguiente pseudo algorítmo llamado el Método de la Bisección: 

Suponga que es una función continua y que a, b son dados tales que f(a)f(b)£0 y e>0 es también dado (criterio de paro).

1. Sean a₁=a, b₁=b, n=1.
2. Defina c_n=(a_n+b_n)/2.
3. Si b_n-c_n£e, entonces aceptamos c_n como una raiz aproximada y paramos el proceso.
4. Si signo(f(b_n))×signo(f(c_n))£0, entonces ponemos a_n+1=c_n. De lo contrario ponemos b_n+1=c_n.
5. Ponga n=n+1, y vuelva a (2).

Ejemplo 1: Considere la función f(x)=x²+x-1. Note que como f(0)=-1 y f(1)=1, tenemos que existe una raiz de la ecuación f(x)=0 en el intervalo (0,1). Vamos a aproximar esta raiz con el método de la bisección. Los resultados son como sigue:

La solución correcta a seis cifras calculada con la función fzero de MATLAB es 0.618034. Podemos ver que el método de la bisección aunque progresa hacia la solución, lo hace un tanto lento. Veamos ahora por que esto es asi analizando la convergencia del método.

Análisis de Error: Como f(a)f(b)£0, sabemos que existe un número tal que f(a)=0. Mediante inducción matemática es fácil ver que

              (4.2)

Esto es asi ya que el largo del intervalo se divide a la mitad cada ves que pasamos por el paso (2) del algorítmo. Nuevamente usando inducción matemática obtenemos que

          (4.3)

Observe que como ó tenemos que

      (4.4)

Combinando (4.3) y (4.4) obtenemos que

           (4.5)

lo cual implica que según . La convergencia en (4.5) es lo que se conoce como convergencia lineal con taza razón de convergencia ½. De la desigualdad (4.5) podemos estimar el número de iteraciones necesarias para obtener que . En particular si requerimos que , obtenemos que

        (4.6)

Basados en este análisis de convergencia podemos hacer las siguientes observaciones:

• ¡El método tiene convergencia segura! Esto es dada la condición inicial f(a)f(b)£0, el método converge a una raiz a en [a,b]. Esta propiedad conocida como convergencia global es una de las características fuertes del método de la bisección y la mayoria de los métodos no la poseen.
• El error en las aproximaciones generadas por el método se reduce a la mitad en cada paso.
• La convergencia lineal caracterizada por la ecuación (4.5) es lenta comparada con otros métodos. Esto es asi ya que el método solo usa evaluaciones de la función y comparaciones. Veremos que usando derivadas ó mas infoormación de la función f, podemos asi obtener métodos más rápidos.

El método de la bisección no generaliza al caso de sistemas nolineales debido a que no es posible una generalización del Teorema (1.3) a funciones vectoriales de variable vectorial.

Método de Newton

Suponemos ahora que la función f es diferenciable e incorporamos información de la derivada en el método. Sea pues f ÎC¹. La recta tangente a f en el punto (x₀,f(x₀)) esta dada por la ecuación . Ahora aproximamos a f con esta recta y definimos x₁ como el intercepto en x de la recto, esto es:

      (4.7)

Este proceso lo podemos repetiir ahora con el punto (x₁,f(x₁)), etc., obteniendo asi la recursión

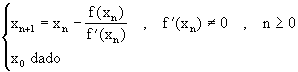           (4.8)

Esta recursión define el Método de Newton y es un ejemplo de una iteración de punto fijo.

Aplicación 1 

Vamos a suponer que queremos calcular el cociente a/b usando solo las operaciones . En la mayoria de las computadoras las operaciones se implementan a nivel de "hardware" mientras que la división se hace mediante programado (software) utilizando. Note que como , entonces es suficiente discutir el computo de reciprocos. Si definimos la función f(x) por

        (4.9)

entonces es la raiz de f(x)=0. Usando que , el método de Newton para la ecuación f(x)=0 toma la forma:

       (4.10)

la cúal envuelve unicamente. Note que

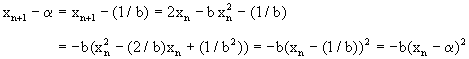
de donde obtenemos la fórmula 

         (4.11)

i.e,

         (4.12)

Esta fórmula, exacta en este caso, aplica en general al método de Newton pero asintoticamente según se converge a la raiz (demostración más adelante). De la ecuación (4.12) obtenemos que según si y solo si , i.e.,

          (4.13)

¿Cómo seleccionamos x₀ para que cumpla con (4.13)? Bueno la parte de x₀>0 es simple de verificar. ¿Cómo saber si x₀<(2/b) cuando no conocemos 2/b? Note que si x₀>0, entonces

Asi que si , entonces sabemos que . En esta caso reducimos x₀, digamos a x₀/2, y empezamos las iteraciones de nuevo. Note que despúes de esta etapa inicial, la convergencia es bién rápida, de hecho cuadrática de acuerdo a la ecuación (4.12). Esto es, en cada iteración el número de cifras significativas se duplica.

Vamos ahora a precisar la noción de rápidez o orden de convergencia de una sucesión.

Definición (4.1): Suponga que la sucesión converge al número a. Decimos que converge a a con orden p³1 si existen M,N³0 tales que

         (4.14)

El número p, que no tiene que ser un entero, se llama el orden de convergencia. Si p=2 la convergencia se llama cuadrática. Si p=1 y M<1 la convergencia se llama lineal con taza o razón de convergencia M.

Nota: Mientras más grande sea p, más rápido converge la sucesión a a. Si p=1, mientras más pequeño sea M, más rápido converge la sucesión.

Aplicación 2

Vamos a discutir ahora el problema de calcular raices cuadradas. Defina para a>0 la función la cual tiene como una de sus raices. Dado que tenemos que el método de Newton aplicado a la ecuación f(x)=0 toma la forma:

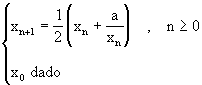              (4.15)

Tenemos ahora el siguiente resultado sobre la convergencia de estas iteraciones.

Teorema (4.1): La sucesión (x_n) definida por la iteración (4.15) converge a para cualquier x₀>0 con orden de convergencia de dos.

Demostración: Si x₀>0 y a>0 entonces sigue de (4.15) que x_n>0 para toda n³0. Además 

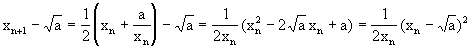         (4.16)

De aqui y como x_n>0, obtenemos que para toda n³1. Ahora (4.15) se puede rescribir como

           (4.17) 

Esto combinado con para toda n³1 implica que para toda n³1. Tenemos pues que (x_n) esta acota inferiormente por y es decreciente de modo que es convergente. Falta ver que converge a. Sea a el limite de (x_n). Entonces dejando en la ecuación (4.17) obtenemos que , i.e, . Pero como x_n>0 para toda n³0, tenemos que , i.e., . La convergencia cuadrática de la sucesión sigue ahora de la expresión (4.16).

Nuevamente vemos convergencia cuadrática del método de Newton. Veamos ahora el resultado general.

Teorema (4.2) (Convergencia Local del Método de Newton): Suponga que es una función C² en una vecindad del número a para el cual . Entonces si x₀ se selecciona suficientemente cerce de a, las iteraciones del Método de Newton convergen a a. Además

          (4.18)

es decir, (x_n) converge a a con orden de convergencia p=2.

Demostración: Usando el Teorema de Taylor podemos escribir

         (4.19)

donde esta entre a y x_n. Como y es continua, existe un intervalo I alrededor de x=a tal que para . Defina ahora el número M por

           (4.20) 

el cual existe y es finito (¿por qué?). Si , podemos despejar para a en (4.19) obteniendo asi que

          (4.21) 

Definimos ahora el intervalo por 

            (4.22)

Veamos ahora que si , entonces para toda n³0. De hecho de (4.21) tenemos que si , entonces . Multiplicando por M ambos lados obtenemos que

          (4.23)

Ahora como , tenemos que . También de (4.23) obtenemos que , i.e, . Combinando esto con obtenemos que . De aqui que si entonces las iteraciones del Método de Newton estan bien definidas, permanecen en , y (4.23) implica que

            (4.24)

Si de modo que , entonces (4.24) implica que y la convergencia es de orden dos ya que . Para terminar note que (4.21) se puede escribir como

             (4.25) 

Dejando y usando que , y por consiguiente , y la continuidad de , obtenemos la expresión (4.18).

La selección del punto inicial x₀ que garantice la convergencia del Método de Newton es un asunto notrivial. Cualquier estimado o conocimiento previo de la localización de la raiz debe utilizarce para asegurar la convergencia del método. Por ejemplo una gráfica de la función f podria arrojar una idea sobre la raiz. Luego de esto se puede utilizar un método como la bisección para corregir la aproximación y pasarla entonces al método de Newton. Esto asemeja a los métodos predictor-corrector comunes en la solución numérica de ecuaciones diferenciales ordinarias. 

Una ves tenemos un método iterativo como el de Newton que no tiene en general una expresión como (4.6) para predecir el número de iteraciones necesarias para lograr un error pre-determinadado, ¿cómo detenemos las iteraciones? Veamos ahora un criterio heurístico para detener el método. Suponiendo que las iteraciones (x_n) estan "cerca" de la raiz a, podemos escribir

          (4.26)

Asi que si tenemos aproximadamente t cifras significativas en x_n como aproximación de a.

Método de la Secante 

La motivación del método de la secante viene de que en ocaciones es complicado ó quizas imposible calcular la derivada de la función f en el método de Newton. Por ejemplo la función f podría estar especificada por un número discreto de puntos ó dada por un programa de computadora. En tales situaciones el método de Newton se hace impractico y buscamos un método intermedio entre el de la bisección y el de Newton. Para esto suponemos que tenemos dos aproximaciones x₀, x₁ de la raiz a. Podemos ahora construir la secante a la función f en los punto (x₀,f(x₀)), (x₁,f(x₁)), la cual esta dada por:

          (4.27)

Definimos la nueva aproximación x₂ como el intercepto en x de esta secante, i.e., 

             (4.28)

Este proceso lo podemos repetir ahora con x₁, x₂ para generar x₃, etc. Obtenemos asi la recurción que define el Método de la Secante:

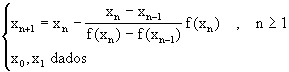           (4.29)

El método de la secante es un ejemplo de un método iterativo de dos puntos ya que predice en el paso n+1 basado en la información obtenida en los pasos n, n-1. Note también que

          (4.30)

de modo que el método de la secante se puede ver como una discretización del método de Newton.

El análisis de convergencia del método de la secante es un tanto más complicado que el del método de Newton y requiere del concepto de diferencias divididas las cuales se discuten en el Cápitulo 5. Usando propiedades de las diferencias dividas se puede demostrar que las iteraciones del método de la secante satisfacen:

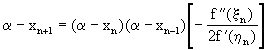          (4.31)

donde esta entre x_n-1, x_n y y pertenece al intervalo minimo que contiene a x_n-1, x_n, a.Usando esta fórmula se puede demostrar el siguiente teorema.

Teorema (4.3) (Convergencia Local del Método de la Secante): Suponga que es una función C² en una vecindad del número a para el cual . Entonces si x₀, x₁ se seleccionan suficientemente cerce de a, las iteraciones del Método de la Secante convergen a a. Además 

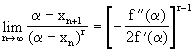            (4.32)

donde .

Demostración (borrador): Vamos a suponer que las iteraciones convergen. Entonces de (4.31), para n suficientemente grande, podemos escribir 

        (4.33)

Multiplicando esta aproximación por M en ambos lados, definiendo , y convirtiendo la aproximación en una igualdad, obtenemos la relación: 

             (4.34) 

donde por conveniencia hemos tomado F₀=F₁=1. La iteración (4.34) define los números de Fibonachi y es bien conocido que para n grande: 

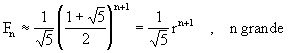            (4.35) 

Asi que

           (4.36)

donde usamos la notación . Ahora podemos escribir

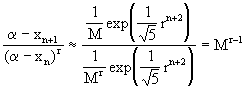           (4.37)

lo cual nos da en forma asintótica la fórmula (4.32).

En la siguiente tabla resumimos las propiedades de los métodos de Newton y de la Secante:

Si es dificil o imposible de evaluar, entonces el método de la secante podría ser más conveniente que el de Newton. Muchas veces f esta dada por una tabla o programa de computadora lo que hace el calculo de imposible. Si es accesible y computacionalmete viable, entonces el método de Newton es preferible por su convergencia rápida. Note que en ambos métodos aproximamos la función original por una función lineal a la cual es fácil de calcular sus raices.

Raices Multiples

En ambos de los Teoremas (4.2) y (4.3) tenemos la condición que garantiza que la función f(x) corta el eje de "x" en en forma transversal. Cuando esta condición de transversalidad no se cumple en la raiz , entonces el método numérico puede diverger o si converge lo hace más lento que en el caso transversal. Vamos a estudiar esta situación en mas detalles en particular para el método de Newton.

Sea f una función, a un número real tal que , y m un entero positivo. Decimos que a es una raiz de f de multiplicidad m si existe una función g(x) tal que 

           (4.38)

Si m=1 decimos que la raiz a es simple. Tenemos ahora:

Teorema (4.4): Sea y . Entonces a es raiz de f de multiplidad m si y solo si

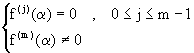             (4.39)

Demostración: Supongamos que (4.39) es cierta. Por el Teorema de Taylor tenemos que podemos escribir:

Como , esta entre a y x, y , tenemos que para x suficientemente cerca de a la función . Asi que con , la ecuación (4.38) se cumple, i.e., a es raiz de f de multiplicidad m.

Suponga que por el contrario, (4.38) es dado donde . Entonces usando la regla de Leibnitz obtenemos que

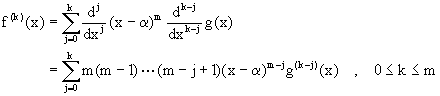             (4.40)

Si y , entonces y (4.40) implica que Si k=m, entonces (4.40) se puede escribir como

Note que al evaluar en los terminos en la sumatoria son todos cero ya que las potencias de son todas positivas. De modo que tenemos que . Combinando esto con lo anterior, obtenemos (4.39).

Ejemplo 2: Para f(x)=(x-2)³(x-1)² tenemos que a =2 es raiz de f de multiplicidad 3 y que a =1 es raiz de multiplicidad 2. Para la función f(x)=sen(x) tenemos que a =0 es una raiz de f. Ademas con 

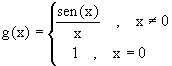
tenemos que a =0 es raiz simple de f. 

Cuando los métodos de Newton ó la Secante se utilizan en problemas con raices multiples, la convergencia si alguna se hace más lenta. Por ejemplo si consideramos el problema de buscar las raices de la ecuación x³=0 usando el método de Newton, entonces las iteraciones de Newton estan dadas por la recursión:

Como a =0 es la única solución en este caso, vemos que el método tiene convergencia lineal en este problema. En general se puede demostrar que si x=a es una raiz de multiplicidad m de la ecuación f(x)=0, entonces las iteraciones del método de Newton convergen localmente a la raiz x=a y satisfacen 

             (4.41)

i.e., la convergencia es lineal si m>1 con taza o razón de convergencia l . Note que si m>2, entonces l >1/2 y el método de la bisección es en general más rápido que el de Newton.

Otro problema con el cálculo de raices multiples es provocado por la aritmética finita de la computadora y el hecho de que la función f no cruza el eje de x transversalmente en x=a . Esto hace que el intervalo de incertidumbre para el cálculo de la raiz sea mucho mayor de lo que sería para una raiz simple.

¿Cómo podemos entonces calcular raices multiples en forma efectiva? Si la multiplicidad m de la raiz es conocida, entonces podemos mejorar la convergencia del método de Newton de dos formas:
 

1. Calculamos la sucesión (x_n) mediante la recurrencia

              (4.42)

   Se puede demostrar (ver …) que con orden p=2. Pero el problema de la incertidumbre mencionado arriba, no mejora debido a que la raiz multiple de f esta todavia presente.

2. Calculamos analiticamente f^(m-1)(x) y le aplicamos el método de Newton a la función F(x)= f^(m-1)(x). Note que ahora a es raiz simple de F, tenemos convergencia cuadrática y no hay el problema de un intervalo de incertidumbre grande. Este método es efectivo si las derivadas de f son fáciles de calcular.

Para estimar m si este no es conocido, usamos el método de Newton aplicado a la función original f y vamos calculando los cocientes 

          (4.43)

los cuales de acuerdo a la fórmula (4.41) aproximan a . Usando esto podemos aproximar "m" y luego procedemos con uno de los métodos (1) ó (2) descritos arriba.

Sistemas Nolineales 

Consideramos ahora el problema de resolver un sistema de ecuaciones nolineales de n ecuaciones en n desconocidas. Sean funciones (nolineales) suficientemente diferenciables. Un sistema nolineal n´ n consiste de:

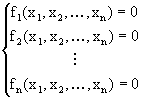             (4.44)

Si definimos por , entonces podemos escribir (4.44) en forma vectorial como:

             (4.45)

Sea tal que , i.e., una solución de (4.45). Defina la siguiente matriz n´ n por

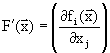             (4.46)

Suponga que es una aproximación de . Entonces usando el Teorema de Taylor para funciones de varias variables, podemos escribir

Definimos ahora la siguiente aproximación como la solución de 

i.e.,

De esta forma continuamos obteniendo asi la versión para sistemas del Método de Newton dada por

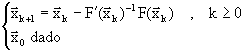              (4.47)

Si es nosingular, y se toma suficientemente cerca de , entonces se puede demostrar que las iteraciones convergen a la raiz . Las iteraciones (4.47) se pueden rescribir para que no haya que calcular el inverso de una matriz. Esto se hace de la forma:

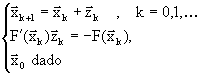          (4.48)

Ejemplo 3: Considere el problema de aproximar una solución del sistema:

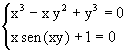
Tenemos que 

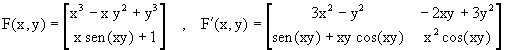
Estas dos expresiones las calculamos en MATLAB mediante las siguientes funciones:

function z=f(w)
z=zeros(2,1);
x=w(1);y=w(2);
z(1)=x^3-x*y^2+y^3;
z(2)=x*sin(x*y)+1;

function z=fp(w)
z=zeros(2,2);
x=w(1);y=w(2);
z(1,1)=3*x^2-y^2;
z(1,2)=-2*x*y+3*y^2;
z(2,1)=sin(x*y)+x*y*cos(x*y);
z(2,2)=x^2*cos(x*y);

Tomando como , tenemos el siguiente programa que implementa la recursión (4.48):

x0=[1,0]';
normx=1;
normz=1;
while normz > 1.0e-6*normx
f0=f(x0);
fp0=fp(x0);
z=-fp0\f0;
normz=norm(z,2);
normx=norm(x0,2);
x0=x0+z;
end
x0

con el cual obtenemos (1.1674,-0.8812) como una raiz aproximada del sistema.

Ejercicios

1. Calcúle la raiz más grande de la ecuación

    

   Despúes de haber calculado la raiz mayor, use división sintética y calcúle las raices restantes. 

2. La siguiente ecuación tiene una raiz única en el intervalo (-1,0):

   

   Use el Método de Newton para calcular la raiz lo más preciso posible para los valores de B=1, 5, 10, 25, 50. Como punto inicial puede tomar entre otros x₀=0. Explique cualquier diferencia en el comportamiento del método según aumenta el valor de B. Utilice la gráfica de para sustentar sus argumentos.

3. Implemente el Método de Newton para buscar todas las raices de un polinomio p(x). Debe utilizar el Método de Horner para evaluar p(x) y su derivada . Si a es una raiz, como resultado del Método de Horner, se obtiene un polinomio q(x) tal que p(x)=(x-a )q(x). Usando q(x) podemos calcular las raices restantes de p(x). Uttilice su programa para resolver las ecuaciones:
   1. 
   2. 
   3. 
4. Sea A la matriz 3x3 y b el vector 3x1 dados por:

   

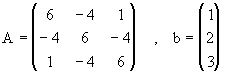
   Escriba un algorítmo (en MATLAB) basado en el método de la bisección, que aproxime a 12 cifras significativas el valor de tal que la solución x de satisfaga . Puede suponer la existencia de una subrutina solve que dada una matriz C y un vector d, solve(C,d) devuelve como resultado la solución z de Cz=d.

   Ayuda: La solución x de se puede ver como una función la cual al sustituirse en la ecuación produce la ecuación (nolineal) en :

   .

5. La ecuación define a y implicitamente como función de x. La función tiene un máximo para . Demuestre que las coordenadas del máximo satisfacen las ecuaciones:

   

   Calcule una solución aproximada de este sistema usando el Método de Newton.

6. Considere el problema de resolver la ecuación integral

   

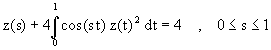
   para la función desconocida z(s). Usando una regla de cuadratura apropiada para discretizar el integral en esta ecuación, obtenga un sistema de ecuaciones nolineales cuya solución es una aproximación de z(s). Resuelva el sistema resultante usando el Método de Newton.