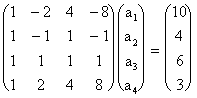
Problema básico de Interpolación: Dados los datos (xi,yi) , 1<=i<=n, queremos hallar una función g(x) tal que
Problema de Interpolación Polinomial: Dados los datos (xi,yi) , 1<=i<=n, queremos hallar un polinomio pn-1(x) de grado a lo más n-1, tal que
Ejemplo: Considere los datos (-2,5), (1,3). Podemos construir el polinomio de grado uno que interpola a estos datos:
Note que también podemos interpolar con una función de la forma
g(x)= a ebx. De hecho b= -(1/3)ln(5/3) y
a=3(5/3)1/3.
Existencia y construcción de pn-1(x)
Considere el caso de los datos (-2,10), (-1,4),(1,6), y (2,3). Entonces si escribimos p3(x)=a1+a2x +a3x2+a4x3 tenemos que
p3(-2)=10 implica que
a1-2a2+4a3-8a4 =10;
p3(-1)=4 implica que
a1-a2+a3-a4 =4;
p3(1)=6 implica que
a1+a2+a3+a4 =6;
p3(2)=3 implica que
a1+2a2+4a3+8a4 =3;
Esto es equivalente al sistema:
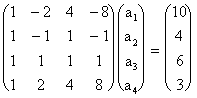
el cual se puede resolver con el siguiente codigo en MATLAB:
y=[10 4 6 3]';
V=[1 -2 4 -8;1 -1 1 -1;1 1 1 1;1 2 4 8];
a=V\y
obteniendo asi el resultado: a=[4.5000 1.9167 0.5000 -0.9167]
Esto generaliza al caso general como sigue. Escribimos pn-1(x)=a1+a2x +...+anxn-1. Ahora
Esto es equivalente al sistema:

La matriz de coeficientes de este sistema se conoce como la matriz de Vandermonde y se puede demostrar que es nosingular si los xi's son todos distintos. (Esta condición se asumirá de aqui en adelante). De modo que el polinomio de interpolación pn-1(x) existe por construcción. La unicidad de pn-1(x) se verifica usando el Teorema Fundamental del Algebra. De hecho, si q(x) es otro polinomio de grado n-1 que interpola a los datos, entonces pn-1(x)-q(x) es polinomio de grado n-1 con n raices, los xi's. Esto es imposible a menos que q(x)= pn-1(x).
Para calcular la matriz de Vandermonde V, primero observamos que si j>1, la columna j de V se obtiene multiplicando (componente a componente) el vector columna (x1,…,xn) con la columna j-1 de V:
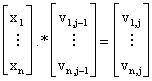
lo cual se puede escribir en MATLAB como V(:,j)=x.*V(:,j-1), donde x=[x1 x2 … xn].
Esto motiva el siguiente programa en MATLAB para calcular los coeficientes de pn-1(x). Aqui x, y son vectores de n componentes y x tiene todos sus componentes distintos:
function a = interpV(x,y)
n=length(x); V=ones(n,n);
for j=2:n
V(:,j)=x.*V(:,j-1);
end
a=V\y;
El polinomio pn-1(x) se puede evaluar ahora usando el método de Horner el expresa a pn-1(x) en su forma anidada:
Dado un valor de z para evaluar pn-1(z) podemos hacer esto mediante el siguiente codigo en MATLAB:
n=length(a); % a es el vector de
coeficientes
pval=a(n);
for i=n-1:-1:1
pval=a(i)+z*pval;
end
Este programa lo podemos generalizar al caso en que z es un vector columna de valores en el que tenemos que evaluar el polinomio:
function pval=hornerV(a,z)
n=length(a); m=length(z);
pval=a(n)*ones(m,1);
for k=n-1:-1:1
pval=a(k)+z.*pval;
end
Ejemplo: Considere el caso de los datos (-2,10),(-1,4),(1,6), y (2,3) que vimos anteriormente. Podemos calcular el polinomio de interpolación mediante:
x=[-2 -1 1 2]'; y=[10 4 6 3]';
a=interV(x,y);
x0=linspace(-2,2,100)';
y0=hornerV(a,x0);
% grafica el polinomio de
interpolación
plot(x0,y0)
Representación de Newton de pn-1(x)
El polinomio de interpolación pn-1(x) es único. De modo que podemos buscar formas más eficientes de calcularlo sin peligro de obtener otro polinomio. La representación de Newton de p n-1(x) es tal que el sistema para obtener los coeficientes es triangular inferior. Esto es una gran ventaja ya que la matriz de Vandemonde es densa y en general mal-acondicionada.
En el caso de los datos (-2,10),(-1,4),(1,6), y (2,3), en lugar de buscar p3(x) de la forma a1+a2x+a3x2+a4x4 lo buscamos de la forma:
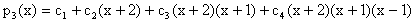
Note ahora que
10 = p3(-2) = c1
4 = p3(-1) = c1 + c2
6 = p3(1) = c1 +3 c2+ 6 c3
3 = p3(2) = c1 +4 c2+ 12 c3 +
12 c4
Esto es un sistema triangular inferior cuya solución es:
c1=10 , c2=-6 , c3=7/3 , c4=-11/12
En el caso general buscamos pn-1(x) de la forma:

Examinamos el caso n=4 para luego llegar al caso general. En este caso al aplicar las condiciones de interpolación pn-1(xi)=yi , 1<=i<=n, obtenemos el sistema triangular superior 4x4 dado por:
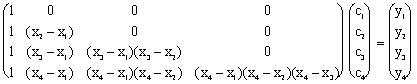
Inmediatamente vemos que c1=y1. Restandole la primera fila a las ecuaciones dos, tres y cuatro y diviendo estas por (x2-x1), (x3-x1), (x4-x1) respectivamente, obtenemos el sistema transformado:
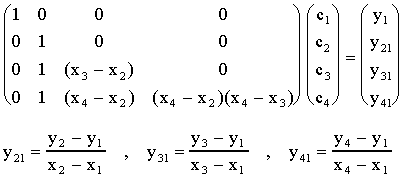
Note que hemos reducido el problema 4x4 a el problema 3x3:
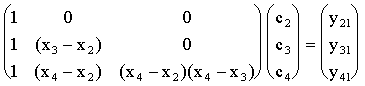
Este sistema corresponde al polinomio
q(x)=c2+c3(x-x2)+c4(x-x2)(x-x3)
que interpola a los datos (x2,y21), (x3,y31) , (x4,y41). Es fácil ver también que
p3(x)=c1+(x-x1)q(x).
Note que el lado derecho de este sistema se puede calcular mediante el siguiente código en MATLAB:
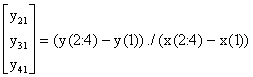
En el caso general tenemos que c1= y1 y que pn-1(x)=c1+(x-x1)q(x) donde q(x) es polinomio de grado n-2 que interpola a los datos:
(xi,(yi-y1)/(xi-x1)) , 2<=i<=n.
Esto nos lleva a el siguiente programa recursivo en MATLAB para calcular la representación de Newton del polinomio de interpolación:
function c = interpNR(x,y)
n=length(x);
c=zeros(n,1);
c(1)=y(1);
if n>1
c(2:n)=interpNR(x(2:n),(y(2:n)-y(1))./(x(2:n)-x(1)));
end
Repitiendo el proceso que nos llevo a la forma recursiva del algorítmo anterior, podemos resolver dicha recursión para obtener asi la forma secuencial del algorítmo para la representación de Newton del polinomio de interpolación:
function c = interpN(x,y)
n=length(x);
for k=1:n-1
y(k+1:n)=(y(k+1:n)-y(k)) ./
(x(k+1:n)-x(k));
end
c=y;
La representación de Newton del polinomio de interpolación se puede evaluar con una variación de método de Horner donde escribimos el polinomio es forma anidada como sigue:
En el caso n=4 esto reduce a :
p3(x)=c1+(x-x1)(c2+(x-x2) (c3+c4(x-x3)))
Esto nos lleva a el siguiente programa en MATLAB que implementa esta versión del método de Horner:
function pval = hornerN(c,x,z)
n = length(c);
pval = c(n)*ones(size(z));
for k = n-1:-1:1
pval=c(k) + (z-x(k)) .* pval;
end
Eficiencia
En general interpNR y interpN requieren menos operaciones de punto flotante que interpV, O(n2) en comparación con O(n3), ya que la matriz de Vandermonde es densa mientras que en la representación de Newton resolvemos un sistema triangular. Hay métodos alternos que resuelven el sistema de Vandermonde en O(n2) operaciones al aprovechar su estructura particular.
Si comparamos interpNR y interpN, el segundo método es más eficiente en el uso de memoria que el primero. La naturaleza recursiva de interpNR requiere O(n2) lugares de memoria en comparacion con O(n) para interpN.
Error de Interpolación
Teorema: Suponga que pn-1(x) interpola a la función f(x) en los puntos distintos x1,…,xn y que f tiene derivadas continuas hasta orden n en un intervalo I que contiene a los xi's. Entonces para cualquier z en I existe un h entre z y los xi's tal que:
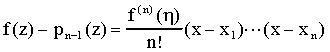
Si f(x) es una función en [a,b] y los xi's estan uniformemente distribuidos en [a,b], i.e.,
entonces se puede demostrar que:
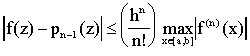
De modo que si
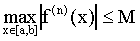
donde M es una constante independiente de n, entonces el error de interpolación tiende a cero según h se va a cero, i.e., hay convergencia. Este es el caso, por ejemplo para las funciones trigonométricas sen y cos, y para la exponencial ex en un intervalo finito.
Esta propiedad (derivadas de todo orden acotadas uniformemente) no la poseen todas las funciones. El ejemplo clásico de este mal comportamiento en las derivadas es la función de Runge dada por:
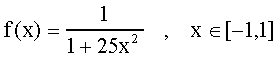
El siguiente programa en MATLAB calcula los polinomios de interpolación de f(x) de grados 10,11,12, y 13 y los grafica en el mismo sistema de coordenadas junto con f(x).
x=linspace(-1,1,100)';
y=1./(1+25*x.^2);
k=0;
for n=10:13
k=k+1;
xunif=linspace(-1,1,n)';
yunif= 1./(1+25*xunif.^2);
cunif=interpN(xunif,yunif);
pvals=hornerN(cunif,xunif,x);
subplot(2,2,k)
plot(x,y,x,pvals)
title(sprintf('(n = %2.0f)',n))
end
Ejercicios
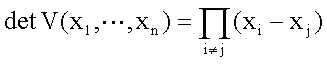
y pn-1(x) interpola a (xi,yi) , 1<=i<=n, entonces
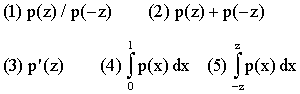
entonces

