Consideramos ahora el problema de aproximar o "ajustar" una función en un número grande de datos que contienen posiblemente un cierto grado de error. En lugar de tratar de ajustar un polinomio de alto grado o insistir en interpolar datos que sabemos tienen un cierto grado de error, lo que hacemos es que buscamos una función que en cierto sentido suavice las fluctuaciones en los datos y a la ves resalte las caracteristicas esenciales de estos. En el método de cuadrados minimos, se trata de minimizar la suma de los cuadrados de las diferencias entre los datos y la función que se usa para aproximar estos.

Suponga que los datos estan dados por donde k=1,2,…m. La función que usamos para aproximar estos datos tiene la forma general:

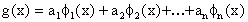
donde las funciones son funciones dadas y los son desconocidas. Un caso común es tomar y en este caso decimos que buscamos aproximar los datos con un polinomio de grado a lo más n-1. Las diferencias entre los datos y la función g(x) estan dados por:

.

Buscamos pues minimizar la suma de los cuadrados de estas diferencias dada por:

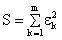
Bajo ciertas condiciones en los datos , los valores de que minimizan a "S" son solución del sistema lineal (ecuaciones normales):

donde

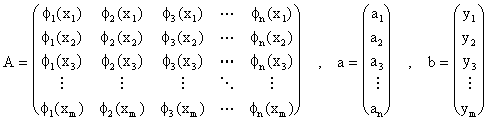
La solucion "a" de las ecuaciones normales se conoce como la solución de cuadrados minimos para los datos usando las funciones base . En el caso el problema de minimizar "S" se conoce como el problema de cuadrados minimos polinomial y la matriz A toma la forma:

.

(Compare esta matriz con la matriz de Vandermonde que vimos en la interpolación de polinomios). Siguiendo nuestra discusión anterior de la matriz de Vandermonde, podemos escribir el siguiente codigo en MATLAB que calcula la matriz A:

function a=vandg(n,x);
m=length(x);
a=ones(m,n);
for j=2:n
a(:,j)=x.*a(:,j-1);
end

El siguiente programa en MATLAB llama la función de arriba para luego ensamblar las ecuaciones normales y resuelve estas para obtener asi la solución de cuadrados minimos:

function a=leastsqu(n,x,y);
A=vandg(n,x);
B=A'*A;
a=B\(A'*y);

El vector "a" que devuelve esta función representa los coeficientes del polinomio de grado a lo más n-1 que mejor aproxima a los datos en el sentido de los cuadrados minimos. Podemos ahora utilizar la función hornerV discutida anteriormente para evaluar dicho polinomio.

Ejemplo: Para ilustrar las ideas presentadas hasta ahora, considere el caso de aproximar 17 datos tomados de la función y=e^x en el intervalo [0,4] utilizando un polinomio cuadrático y otro cúbico:

%
% Genera los datos
%
x=[0:.25:4]';
y=exp(x);
%
% Calcula los coeficientes de los polinomios cuadrático y cúbico
% que mejor aproximan en el sentido de los cuadrados minimos
%
a2=leastsqu(3,x,y);
a3=leastsqu(4,x,y);
%
% Genera puntos adicionales para evaluar los polinomios y
% la función original
%
xx=[0:.02:4]';
%
% Evalua los polinomios y la función original
%
pval2=hornerV(a2,xx);
pval3=hornerV(a3,xx);
yy=exp(xx);
%
% Traza las gráficas
%
plot(xx,yy,xx,pval2,xx,pval3,x,y,'o')
xlabel('X');ylabel('Y');
title('Cuadratica en violeta; Cubica en azul; exp(x) en amarillo')

La matriz de coeficientes de las ecuaciones normales es en general una matriz mal acondicionada según la "m" aumenta. De hecho en el caso del problema de cuadrados minimos polinomial, es fácil ver que la entrada (k,l) de es de la forma:

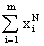
donde la N=k+l-2 . Pero

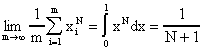
de modo que

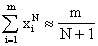
para "m" grande. Asi que es (aproximadamente) proporcional a la matriz de Hilbert de orden nxn para "m" grande la cual es mal acondicionada. El número de datos no tiene que ser muy grande. De hecho en el ejemplo anterior, los numeros de condición de son 983.3594 y 5.7299e+004 respectivamente para los casos n=3,4 lo cual indica que se pierden en el orden de 4 cifras significativas en el calculo.

Para poder resolver las ecuaciones normales en forma eficiente y estable, se utiliza la llamada factorización QR de la matriz A.

Teorema: (Factorización QR) Sea A una matriz mxn de rango n. Entonces existe una matriz Q de tamaño mxn con , y una matriz R de tamaño nxn triangular superior y nosingular tal que A=QR.

La demostración de este teorema utiliza el proceso de Gram-Schmidt y se encuentra por ejemplo en el libro Linear Algebra with Applications de S.J. Leon. Tampoco discutiremos los aspectos computacionales de como calcular la factorización QR de una matriz pues utilizaremos las funciones de MATLAB para esto. Lo que si nos interesa en este punto es que utilizando la factorización QR de la matriz A que aparece en las ecuaciones normales, podemos calcular la solución de cuadrados minimos en forma eficiente y sin problemas de mal acondicionamiento.

Teorema: Sea A una matriz mxn de rango n y A=QR la factorización QR de A dada por el teorema anterior. Entonces la solución "a" de las ecuaciones normales se puede obtener resolviendo el sistema triangular .

Demostración: Dado que A=QR tenemos que:

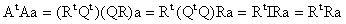
De igual forma: . Como R es nosingular R^t también lo es y tenemos pues que es equivalente al sistema . <>

Vale la pena recalcar que los sistemas triangulares se resuelven eficientemente mediante sustitución para atras y son por lo general bien acondicionados. La función qr de MATLAB se utiliza para calcular las factorizaciones QR. Modificamos la función leastsqu de arriba como sigue:

function a=leastsqr(n,x,y);
A=vandg(n,x);
[Q R]=qr(A);
a=R\(Q'*y);

El mismo ejemplo anterior pero usando esta subrutina en lugar de leastsqu produce resultados similares (al número de cifras mostradas) pero ahora los números de condición de R son 31.3586 y 239.3714 para n=3,4 respectivamente los cuales son mucho mejor que antes.

Ejercicios:

1. Considere los datos dados por los vectores x=[0:0.25:3], y=[6.3806 7.1338 9.1662 11.5545 15.6414 22.7371 32.0696 47.0756 73.1596 111.4684 175.9895 278.5550 446.4441].

   Aproxime estos datos con funciones de la forma:

   1. 
   2. 
   3. 

   Modifique los programas dados anteriormente según sea necesario. Grafique las tres funciones "g(x)" y los datos originales en un mismo sistema de coordenadas. ¿Qué tan bien aproximan estas funciones a los datos?

2. La función se puede aproximar con un polinomio de grado cinco de la forma . Use la función gamma de MATLAB para generar valores de para x=0:0.1:1. Usando los programas desarrollados en esta lección, construya el polinomio de grado cinco que mejor aproxima estos datos en el sentido de los cuadrados minimos. Trace los datos, la función y el polinomio calculado en el mismo sistema de coordenadas.