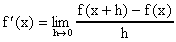
El cálculo de la derivada de una función puede ser un proceso "difícil" ya sea por lo complicado de la definición analítica de la función o por que esta se conoce unicamente en un número discreto de puntos. (Este es el caso si la función representa el resultado de algún experimento). En esta lección estudiaremos técnicas para aproximar las derivadas de una función y veremos el análisis de error de dichas formulas.
Formulas para la primera derivada: La definición de la derivada de una función f(x) en el punto "x" esta dada en terminos del limite:
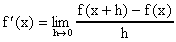
De esta definición podemos decir que si "h" es pequeño entonces:
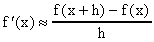
(Note el simbolo de aproximación). Esto nos da inmediatamente la primera formula numérica para aproximar la derivada:
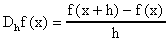
Antes de ver algunos ejemplos donde usamos esta formula, tratemos de constestar la pregunta de ¿cuán buena es esta aproximación de la derivada? Por el Teorema de Taylor sabemos que:
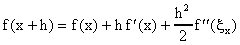
donde 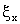
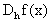
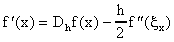
Esta formula nos dice que 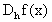
Ejemplo 1: Tomamos 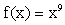
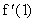
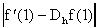
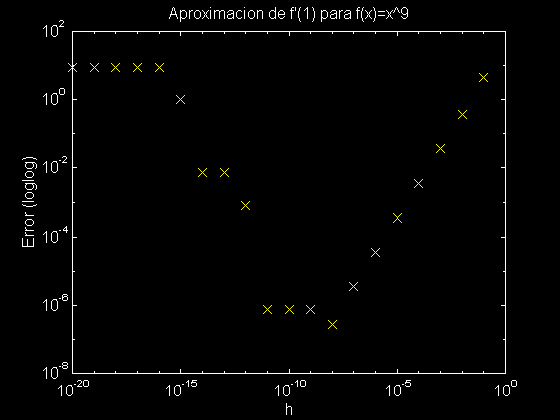
Podemos ver que los errores disminuyen hasta un cierto valor critico "hmin" luego del cual los errores aumentan según la "h" disminuye. ¿Contradice esto el resultado de arriba de O(h) del error? ¡NO! El resultado de arriba es sobre la convergencia si la aritmética es exacta y se dice que es un resultado asintótico. La figura ilustra los efectos de redondeo debido a la aritmética finita los cuales se hacen significativos para "h" pequeño y pueden afectar cualquier formula numérica para aproximar la derivada. Sin embargo, una formula con un grado de aproximabilidad digamos O(h2) es preferible a una O(h) ya que los errores (teoricos) tienden a cero más rápido y asi la "h" no se tiene que hacerse tan pequeña reduciendo asi los efectos de los errores por la aritmética finita. <>
El método de arriba usando la expansión de Taylor se puede utilizar para obtener formulas para aproximar la derivada con un grado de aproximabilidad más alto que uno. Ilustramos esto para la obtención de una formula O(h2). Si en lugar de llegar hasta terminos de orden dos, expandimos hasta terminos de orden tres en la expansión de Taylor, obtenemos las formulas:
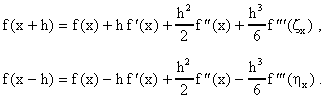
Si restamos estas dos ecuaciones, despejamos para f'(x), y usamos el teorema del valor medio aplicado a f'''(x) obtenemos la formula:
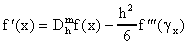
donde
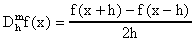
y 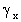
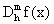
Ejemplo 2: Comparamos las dos formulas obtenidas hasta ahora para
aproximar f'(x) con el ejemplo de 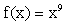
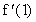
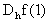
|
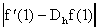
|
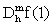
|
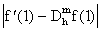
|
|
Este ejemplo ilustra lo superior de la formula 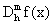
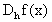
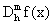
En forma similar se pueden obtener formulas de orden mayor utilizando expansiones de Taylor que envuelvan x±2h, x±3h, etc. Por ejemplo la expansión
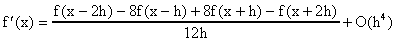
nos da una formula de orden cuatro para f'(x). Es importante observar que mientras más alto el grado de aproximabilidad de la formula, más suave tiene que ser la función para que dicha aproximación sea valida. Por ejemplo esta formula de orden cuatro requiere que la función tenga cinco derivadas continuas en el intervalo en cuestión mientras que la formula de orden dos requiere unicamente tres derivadas continuas.
Formulas para la segunda derivada: El proceso de arriba se puede usar para obtener formulas para las derivadas de orden mayor de uno de una función f(x). Usamos este proceso para obtener una formula para la segunda derivada. Usando el Teorema de Taylor, podemos escribir las expansiones:
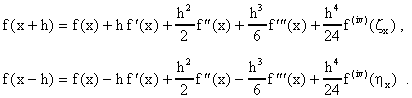
Sumando estas dos expansiones y despejando para f''(x) obtenemos:
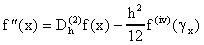
donde
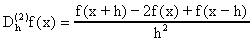
y 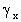
Ejemplo 3: Examinamos la formla de arriba en el caso
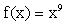
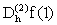
|
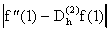
|
|
Nuevamente se puede ver el factor de cuatro en el error, caracteristico de la convergencia de orden dos. <>
En forma similar se pueden obtener formulas de orden mayor utilizando expansiones de Taylor que envuelvan x±2h, x±3h, etc. Por ejemplo la expansión
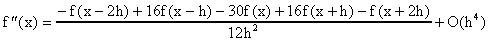
nos da una formula de orden cuatro para f"(x).
Diferenciación usando polinomios de interpolación: Suponga
que 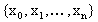
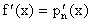
Suponga que 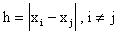
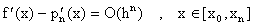
Aunque no discutiremos en más detalles este método para aproximar derivadas, si mencionamos que las dos formulas que discutimos para aproximar f '(x) se pueden obtener usando polinomios de interpolación de grados uno y dos respectivamente.
Ejercicios:
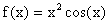 en x=1 y para h=0.1, 0.01.
en x=1 y para h=0.1, 0.01.
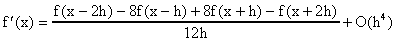
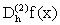 repita un proceso similar al del
Ejemplo 1 donde "h" se disminuye hasta que el error en la formula empieza
a aumentar.
repita un proceso similar al del
Ejemplo 1 donde "h" se disminuye hasta que el error en la formula empieza
a aumentar.
