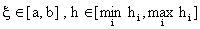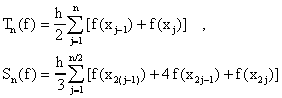
Pasamos ahora a estudiar formalmente el error de aproximación en las fórmulas:

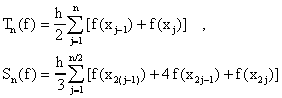
Regla del Trapezoide: Usando el teorema sobre el error de interpolación discutido anteriormente, tenemos que si p₁(x) es el polinomio que interpola a f(x) en x_j-1, x_j entonces

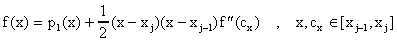
De modo que

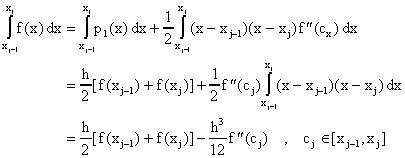
donde usamos el Teorema del Valor Medio para integrales. Tenemos pues que el error en la fórmula del método del trapezoide esta dado por

(*)

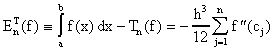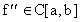
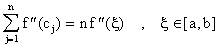
Suponiendo que (continua en [a,b]) y aplicando el Teorema del Valor Medio para funciones, obtenemos que

Usando este resultado en la fórmula del error de arriba obtenemos que

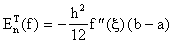
Esta fórmula se conoce como la fórmula exacta del error y establece que la fórmula del trapezoide T_n(f) tiene un orden de convergencia de O(h²) lo que confirma nuestros resultados numéricos de la sección anterior. Esta fórmula aparte de su valía teorica, no nos proporciona un estimador práctico del error ya que f '' puede no ser accesible y el punto x de la fórmula es desconocido. Para obtener un estimador práctico del error utilizamos la llamada fórmula asintótica que se obtiene de la siguiente manera. Si f '' es continua, entonces

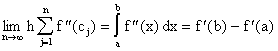
Asi que usando esto y la fórmula (*) obtenemos que

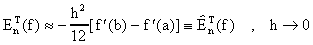
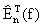
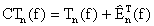
La fórmula se conoce como el estimador asintótico del error. Note que si f ' es accesible, esta fórmula envuelve cantidades conocidas y es posible calcularla como parte del proceso de aproximación. Más aun podemos utilizar el estimador para corregir la fórmula del trapezoide obteniendo asi la fómula del trapezoide corregida:

la cúal en general debe ser una mejor aproximación a I(f) que T_n(f).

Ejemplo 1: Consideremos nuevamente el problema de aproximar

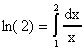
En este caso f(x)=1/x de modo que f'(x)=-1/x², asi que el estimador asintótico del error esta dado por la fórmula

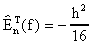
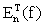
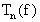
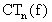
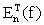
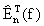
Como en este problema el valor exacto del error se conoce, podemos compararlo con la fórmula asintótica. Veamos los resultados:

n
2	0.708333	0.692708	-0.0151862	-0.015625
4	0.697024	0.693118	-0.00387663	-0.00390625
8	0.694122	0.693145	-0.00097467	-0.000976562
16	0.693391	0.693147	-0.000244022	-0.000244141
32	0.693208	0.693147	-0.0000610277	-0.0000610352
64	0.693162	0.693147	-0.0000152583	-0.0000152588
128	0.693151	0.693147	-3.81467e-006	-3.8147e-006
256	0.693148	0.693147	-9.53672e-007	-9.53674e-007
512	0.693147	0.693147	-2.38418e-007	-2.38419e-007
1024	0.693147	0.693147	-5.96046e-008	-5.96046e-008

Podemos ver de esta tabla que la fórmula asintótica del error predice bastante bien el error real en este ejemplo. También podemos observar que la fórmula corregida del trapezoide produce seis cifras correctas en la aproximación con apenas n=16 mientras que la fórmula sin corregir requiere hasta n=512. <>

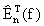
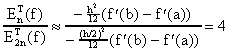
De la fórmula asintótica tenemos que

lo cual fué lo que observamos en nuestros computos numéricos. Note también que si casualmente f '(a)=f '(b) , entonces la convergencia del método será más rápida.

Método de Simpson: En este caso el análisis de los errores es similar al del método del trapezoide pero más extenso. Simplemente pues resumimos los resultados en este caso. Si entonces la fórmula exacta del error esta dada por

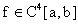
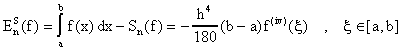
y la fórmula asintótica por

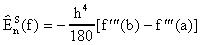
La fórmula corregida de Simpson es pues

De la fórmula del error exacto se obtiene que el método tiene un orden de convergencia O(h⁴) y empleando la fórmula asintótica podemos ver que los cocientes 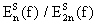son aproximadamente 16.

Ejercicios:

1. Repita los cálculos del Ejemplo 1 pero para el método de Simpson.
2. Para la formulas básica y compuesta de la regla del punto medio (problema 2, sección anterior) haga un análisis de errores y derive las fórmulas exactas y asintóticas del error y la fórmula corregida del método.
3. Si la regla del trapezoide se utiliza para aproximar

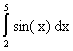
   con h=0.01, halle una cota para el error en dicha aproximación y un estimado asintótico del mismo.

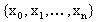4. Si los puntos no estan uniformemente distribuidos en [a,b], es posible generalizar la fórmula del trapezoide en este caso como sigue: sean 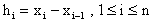. Entonces definimos

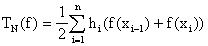
   Verifique la siguiente fórmula para el error exacto de este método

   

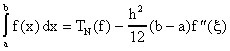
   donde .