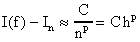
Aqui examinamos dos procedimientos para obtener fórmulas de integración numérica de orden arbitrario. Una de estas técnicas es la extrapolación de Richardson que es un proceso comúnmente utilizado en análisis numérico para acelerar la convergencia de sucesiones convergentes. La otra técnica son las reglas de cuadrátura Gaussiana que producen fórmulas de alto grado utilizando puntos distribuidos en el intervalo de integración en forma no uniforme.
Extrapolacion de Richardson: Denotamos aqui por In cualquier fórmula numérica para aproximar I(f), e.g., la fórmula del Trapezoide ó la regla de Simpson. La correspondiente fórmula asintotica del método nos garantiza que para alguna constante C
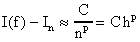
donde p es el orden de convergencia del método, e.g., p=2 para el método del Trapezoide y p=4 para el de Simpson. Podemos escribir ahora que
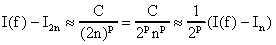
Despejando para I(f) obtenemos que
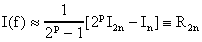
lo cual se conoce como la fórmula de extrapolación de Richardson y se puede demostrar que
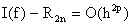
i.e., el orden de la fórmula original se duplicó.
Ejemplo 1: Consideramos nuevamente el computo de
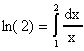
cuyo valor exacto es 0.693147 correcto a seis cifras. El siguiente programa en MATLAB implementa el método de extrapolación de Richardson para la regla del trapezoide:
n=2;
x=linspace(1,2,3);
y=1./x;
iaproxn=trapz(x,y);
for i=2:5
n=2*n;
x=linspace(1,2,n+1);
y=1./x;
iaprox2n=trapz(x,y);
richard=(4*iaprox2n-iaproxn)/3;
disp(['n=' num2str(n) ', iaprox2n=' num2str(iaprox2n,6) ',richard='
num2str(richard,6)])
iaproxn=iaprox2n;
end
Los resultados fueron como sigue:
Aqui podemos ver que ya para n=32 la fórmula de Richardon tiene ya seis cifras correctas. Para el método del trapezoide la fórmula de Richardson es de orden O(h4) y no requiere derivadas de la función f(x) en comparación con la fórmula corregida. <>
La fórmula de extrapolación de Richardson se puede ahora utilizar en forma recursiva generando formulas de orden cada vez más alto (se duplica en cada etapa). La fórmula resultante por este procedimiento se conoce como la fórmula de integración numérica de Romberg.
Reglas de Cuadrátura Gaussiana: Consideramos por el momento integrales de la forma
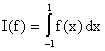
Note que si el integral esta dado en un intervalo arbitrario [a,b] entonces mediante el cambio de variables
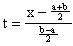
tenemos que
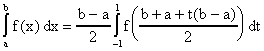
lo cual nos da una integral en [-1,1]. Asi que sin perdida de generalidad podemos asumir que el integral es en [-1,1].
Sean x1,x2,…,xn puntos (no necesariamente uniformemente distribuidos) en [-1,1] y w1,w2,…,wn números llamados pesos ("weights"). Los puntos xj's y los pesos wj's se determinan de modo que la fórmula de integración numérica
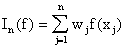
sea exacta para polinomios de grado a lo más 2n-1, i.e., In(p)=I(p) para todo polinomio p de grado a lo más 2n-1. Como In é I son operadores lineales, basta verificar que
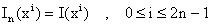
Caso n=1: Aqui I1(f)=w1f(x1) y requerimos que I1(1)=I(1), I1(x)=I(x). Pero I(1)=2 y I1(1)=w1 de modo que w1=2. Además I(x)=0 y I1(x)=2x1, de donde obtenemos que x1=0. Tenemos pues la fómula numérica I1(f)=2f(0) lo cúal se conoce como la fórmula del punto medio.
Caso n=2: Tenemos ahora que I2(f)= w1f(x1)+ w2f(x2) y se requiere que I2(xi)=I(xi) para i=0,1,2,3. Esto nos lleva al siguiente sistema nolineal para x1,x2,w1,w2:
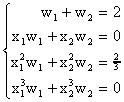
Suponiendo que x1, x2 son conocidas, resolvemos la tercera y cuarta ecuación (que son lineales en los w's) mediante la regla de Cramer para w1, w2 obteniendo asi que
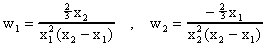
Sustituyendo estas expresiones en la primera y segunda ecuación y resolviendo para x1, x2 obtenemos que
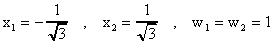
Asi que nuestra fórmula numérica en el caso n=2 lee como sigue:
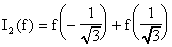
Caso n>2: Al aplicar las condiciones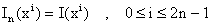 
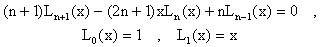
se
obtiene un sistema nolineal de 2n ecuaciones en 2n desconocidas (las x's
y las w's). Este sistema se puede resolver numéricamente usando el
método de Newton para sistemas nolineales. Pero en lugar de proceder
de esta forma se utiliza el hecho de que se puede demostrar que los
xi's son los ceros del n-esimo polinomio de Legendre
Ln(x). Estos polinomios se definen por la recursión
En particular tenemos que L2(x)=(3/2)x2-(1/2) cuyos ceros son ±1/Ö3 que fueron los x's que determinamos en el caso n=2. También
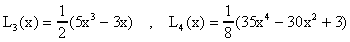
de donde podemos obtener los x's para las fórmulas de los casos n=3,4 respectivamente. Teniendo los x's podemos ahora calcular los w's resolviendo un sistema lineal de ecuaciones.
Ejemplo 2: Aproximamos
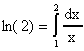
usando la regla de cuadrátura con n=2. Primero hacemos un cambio de variables de modo que el integral sea en el intervalo de [-1,1]. Para esto usamos el cambio de variables discutido al principio de esta sección lo que resulta en:
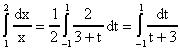
Tenemos ahora que
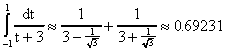
Ejercicios:
