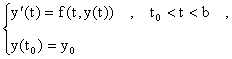
Las ecuaciones diferenciales aparecen naturalmente al modelar situaciones físicas en las ciencias naturales, ingeniería, y otras disciplinas, donde hay envueltas razones de cambio de una ó varias funciones desconocidas con respecto a una ó varias variables independientes. Estos modelos varían entre los más sencillos que envuelven una sola ecuación diferencial para una función desconocida, hasta otros más complejos que envuelven sistemas de ecuaciones diferenciales acopladas para varias funciones desconocidas. Por ejemplo, la ley de enfriamiento de Newton y las leyes mecánicas que rigen el movimiento de los cuerpos, al ponerse en terminos matemáticos dan lugar a ecuaciones diferenciales. Usualmente estas ecuaciones estan acompañadas de una condición adicional que especifica el estado del sistema en un tiempo o posición inicial. Esto se conoce como la condición inicial y junto con la ecuación diferencial forman lo que se conoce como el problema de valor inicial. Por lo general, la solucón exacta de un problema de valor inicial es imposible ó dificil de obtener en forma analítica. Por tal razón los métodos numéricos se utilizan para aproximar dichas soluciones. Comenzaremos discutiendo los métodos para ecuaciones escalares y luego generalizamos los mismos a sistemas de ecuaciones.
El Método de Euler: Considere el problema de valor inicial para la función (desconocida) y(t) descrito por:
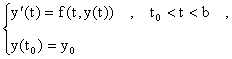
Defina para n³0 los siguientes cantidades:
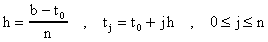
Para cualquier j³0, tenemos por el Teorema de Taylor que podemos escribir:
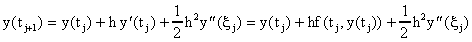
Eliminando los terminos O(h2) obtenemos la aproximación:
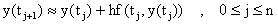
Denotamos ahora por yj una aproximación de y(tj). Entonces motivado por la aproximación de arriba definimos las aproximaciones {yj} por la recursión:
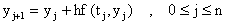
lo que se conoce como el método de Euler. La cantidad
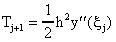
la cual descartamos en la serie de Taylor para obtener las aproximaciones, se llama el error de truncación o local del método de Euler y esta intimamente relacionada con la convergencia del método. De hecho si definimos los errores absolutos por ej=y(tj)-yj, entonces restando la expansión de Taylor y la formula del método se obtiene que
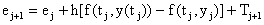
Suponiendo ahora que f cumple una Condición de Lipschitz uniforme en t, i.e.,
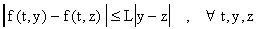
para alguna constante L, entonces se puede verificar que de la recursión de los errores obtenemos que:
(*)
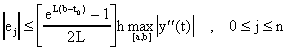lo que prueba que el método tiene un orden de convergencia global O(h).
La implementación en MATLAB del método de Euler es relativamente simple. Hacemos esto mediante una subrutina llamada feuler que recibe en la secuencia de llamada el nombre de la subrutina que calcula la función f, y los datos t0, b, y0, n. Esta subrutina devuelve dos vectores con las t's y las y's aproximadas. Veamos:
function [tvals,yvals]=feuler(f,t0,b,y0,n)
h=(b-t0)/n;
tvals=zeros(1,n+1);
yvals=zeros(1,n+1);
index=[0:1:n];
tvals=t0+h*index;
yvals(1)=y0;
for i=2:n+1
yvals(i)=yvals(i-1)+h*feval(f,tvals(i-1),yvals(i-1));
end
Usamos ahora esta subrutina en el siguiente ejemplo.
Ejemplo 1: Considere el problema de valor inicial
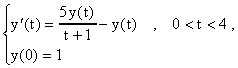
cuya solución exacta es y(t)=(t+1)5e-t. Definimos la siguiente función en MATLAB que evalúa el lado derecho de la ecuación diferencial:
function f=etest(t,y);
f=5*y/(t+1)-y;
Ahora resolvemos este problema para n=20 y gráficamos la solución numérica junto con la exacta para comparar los resultados usando las siguientes instrucciones en MATLAB:
[t,y]=feuler('etest',0,4,1,20);
yy=(t+1).^5.*exp(-t);
plot(t,y,'x',t,yy)
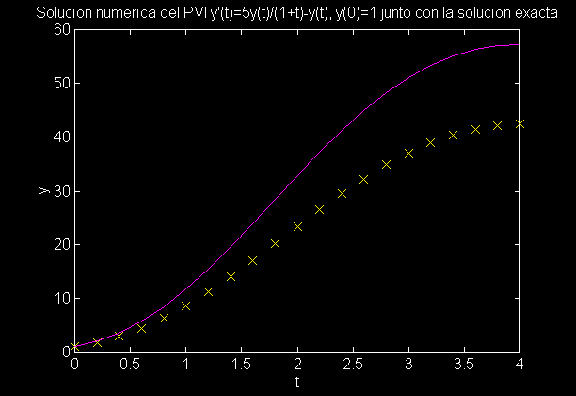
Las soluciones numéricas se ilustran en la figura por las "x". Note que las aproximaciones numéricas no coinciden con la solución exacta y que el error aumenta según aumenta la "t". Esto es lo usual y no contradice el estimado del error (*) de arriba donde el error puede crecer hasta exponencial con respecto al largo del intervalo. Para controlar el error lo primero que se hace es disminuir la h, i.e., aumentar la n. Para este ejemplo mostramos los resultados de disminuir h sucesivamente para la aproximación de y(4)= 57.2364 a las cifras mostradas. Obtuvimos lo siguiente:
Vemos aqui que definitivamente la aproximación mejora según aumenta la "n" pero la convergencia es bastante lenta. De hecho la aproximación numérica tiene apenas un error relativo de 3x10-3 para n=2560, i.e., h=4x10-4. <>
El ejemplo anterior muestra que aunque el método de Euler es convergente según la "h" tiende a cero, la convergencia del método puede ser bien lenta requiriendo un "h" excesivamente pequeño para un error satisfactorio en las aproximaciones. Al usar un "h" excesivamente pequeño en los calculos podemos tener acumulación de errores debido a la aritmética finita similar al fenomeno que observamos en la diferenciación numérica. Esta situación mejora o se puede evitar al considerar métodos con un orden de convergencia más alto como los llamados métodos Runge-Kutta que discutimos más adelante.
Otra noción bien importante en adición a la de convergencia de un método numérico es la de estabilidad absoluta. En este caso la "h" se mantiene fija y nos interesa determinar cúan sensitivo es el método numérico a variaciones en la condición inicial y0.
Ejemplo 2: Considere el problema de valor inicial
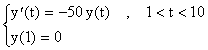
cuya solución exacta es y(t)=0. Resolvemos el mismo problema de valor inicial pero con la condición inicial cambiada a y(1)=10-4 y usamos h=0.05 en el método de Euler. La solución calculada fué como sigue donde mostramos el valor absoluto de la misma:
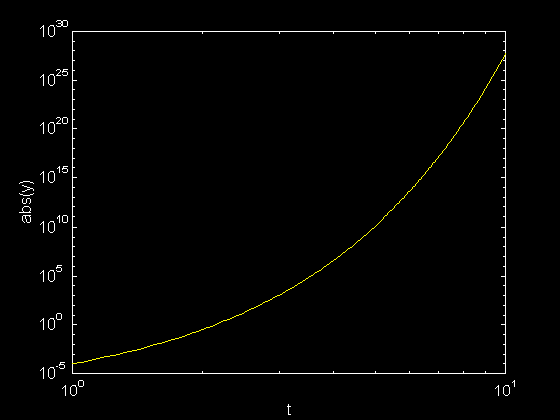
Podemos ver que un error inicial de 10-4 produjo un error de más de 1025 en la aproximación de y(10). En este caso calcular con h=0.025 o n=360 aproximadamente, produce resultados satisfactorios. <>
El ejemplo anterior se generaliza a la ecuación
, donde 
. La solución
de este problema es 
para alguna constante C. Estas
soluciones son acotadas para todo "t". La región de estabilidad
absoluta S de un método se define por el conjunto de las
"hl" tal que las soluciones numéricas sean
acotadas al aplicarse al problema prueba 
.
En el caso del método de Euler tenemos que al aplicar este al problema
prueba, el método reduce a:
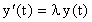
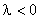
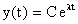
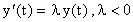
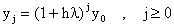
Vemos aqui que las soluciones numéricas estan acotadas para todo "j"
si y solo si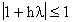 
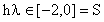
, i.e., 
.
Ejemplo 3: En el Ejemplo 2 donde l=-50,
el requisito de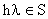 
implica que 
.
Claramente h=0.05 no cumple con esta condición mientras que h=0.025
si la satisface. <>
El método de Euler generaliza en forma directa a sistemas de ecuaciones diferenciales. La teoria de convergencia global y de estabibilidad absoluta que discutimos en el caso de una ecuación, aplica palabra por palabra al caso de sistemas. En la subrutina feuler descrita antes solo hay que añadir una instrucción para determinar el tamaño del sistema. Hicimos un cambio también para que en lugar de "n" la subrutina reciba "h". La subrutina queda ahora como:
function [tvals,yvals]=feuler(f,t0,b,y0,h)
n=floor((b-t0)/h)+1;
m=length(y0);
tvals=zeros(1,n+1);
yvals=zeros(m,n+1);
index=[0:1:n];
tvals=t0+h*index;
yvals(:,1)=y0;
for i=2:n+1
yvals(:,i)=yvals(:,i-1)+h*feval(f,tvals(i-1),yvals(:,i-1));
end
Esta subrutina puede ser usada exactamente como antes para el caso de una ecuación. Veamos un ejemplo numérico de un sistema de ecuaciones y como lo resolvemos con feuler.
Ejemplo 4: Considere el siguiente modélo simplificado del corazón donde x(t) representa el largo de una cierta fibra ó musculo del corazón y s(t) representa un estimulo aplicado:
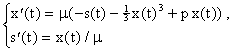
Aqui m y p son parámetros del modélo. El lado derecho del sistema lo evaluamos mediante la siguiente subrutina en MATLAB:
function f=heart(t,y);
%
% y(1) representa x(t) y y(2) representa s(t)
%
global mheart pheart
f=zeros(2,1);
f(1)=mheart*(-y(2)-y(1)^3/3+pheart*y(1));
f(2)=y(1)/mheart;
Note el uso de la instrucción global que declara las variables mheart y pheart como variables globales las cuales son accesibles por cualquier rutina o programa con una instrucción global igual. Usamos las condiciones iniciales x(0)=0, s(0)=-1 y los valores de m=0.5 y p=1. Aproximamos la solución con la siguiente secuencia de instrucciones en MATLAB:
global mheart pheart
mheart=0.5;
pheart=1;
[t,y]=feuler('heart',0,10,[0,-1]',0.1);
plot(t,y(1,:),t,y(2,:))
xlabel('t');ylabel('x(t),s(t)');
title('Modelo del corazon: x(t) en amarillo, s(t) en violeta.')
lo cual produce la siguiente gráfica:
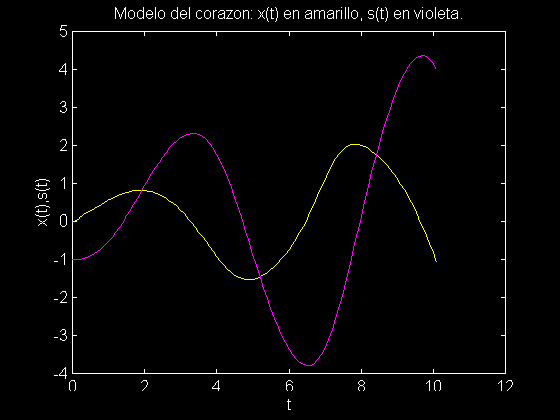
No comentamos sobre las interpretaciones físicas de estas graficas pero si mencionamos que el método de Euler es efectivo en este problema ya que las soluciones no varian muy rapidamente en el intervalo en cuestión. <>
Para resolver ecuaciones diferenciales de orden mayor de uno hacemos primero un cambio de coordenadas para convertir la ecuación dada a un sistema de primer orden. Luego usamos el método de Euler para sistemas según descrito arriba.
Ejemplo 5: Considere el problema de valor inicial para la siguiente ecuación de orden dos:
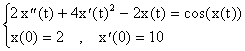
Haciendo la sustitución ó cambio de variables x1(t)=x(t), x2(t)=x'(t), entonces el problema de arriba es equivalente al siguiente sistema de primer orden:
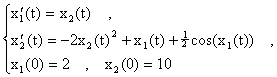
Este sistema puede resuelto de forma similar al que resolvimos en el Ejemplo 4. <>
Ejercicios:
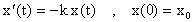
donde k es una constante caracteristica del isótopo radioactívo. Para x0=50 y k=0.05 resuelva este problema de valor inicial en el intervalo [0,10] con h=1,0.1,0.01. Compare sus resultados con la solución exacta que es x(t)=50 exp(-0.05t).
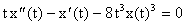a un sistema de orden uno. Resuelva el sistema
resultante en el intervalo [1,4] si las condiciones iniciales son x(1)=1/2,
x'(1)=-1/2. La solución exacta en este problema es
x(t)=1/(1+t2).
