El uso de polinomios de interpolación de alto grado puede producir errores grandes debido al alto grado de oscilación de este tipo de polinomios. Para evitar este problema se aproxima la función desconocida en intervalos pequeños usando polinomios de grado bajo. El caso más común de la interpolación por pedazos es usar polinomios cúbicos.

Polinomios Cúbicos de Lagrange: Suponemos que n es divisible por tres y buscamos un polinomio cúbico que interpole a la función en los puntos . Este polinomio esta dado en su representación de Lagrange por:

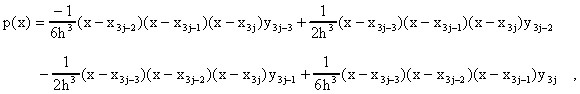
para y se asume constante para toda i.

Interpolación de Hermite: Aqui buscamos un polinomio por pedazos H_n(x) que sea cúbico en cada subintervalo , y que interpole a f(x) y f'(x) en los puntos . La función H_n(x) queda determinada en forma única por estas condiciones y su cálculo requiere de la solución de n sistemas lineales de tamaño 4x4 cada uno. La desventaja de la interpolación de Hermite es que requiere de la disponibilidad de los lo cual no es el caso en muchas aplicaciones.

Interpolación usando Splines: Los dos tipos de polinomios por pedazos que hemos discutidos hasta ahora tienen la desventaja de que su segunda derivada no es continua en los puntos de interpolación. Se ha observado que en aplicaciones gráficas, el ojo humano es capaz de detectar discontinuidades en la segundas derivadas de una función, haciendo que los gráficos con este tipo de funciones no luscan uniformes. Esto motiva el uso de los splines que son funciones s(x) continuas por pedazos con las siguientes propiedades:

1. s(x) es polinomio cúbico en .
2. existen y son continuas en .
3. s(x) interpola a la función f en los datos .
4. s(x) es continua en .

Si escribimos , entonces tenemos un total de 4n desconocidas. Las condiciones 2) y 4) nos dan 3(n-1) ecuaciones mientras que de 3) obtenemos n+1 para un total de 4n-3(n-1)-(n+1)=2 grados de libertad. Estos grados de libertad se fijan imponiendo condiciones de frontera adicionales en s(x).

Defina . Como s(x) es cúbico en , entonces s"(x) es lineal en y esta dado por:

.

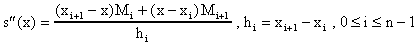Integrando esta ecuación dos veces, obtenemos que

.

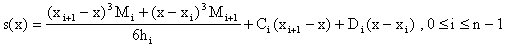Las condiciones implican que

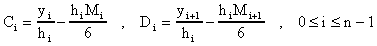
Sustituyendo esto en la formula anterior de s(x) obtenemos que

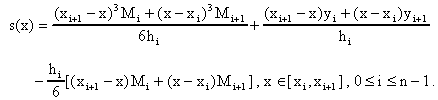
Note que s(x) y s"(x) son continuas por construcción y además tenemos que la condición de interpolación se cumple. Falta la condición de que s'(x) sea continua, i.e.,

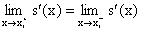
En , tenemos que

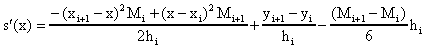
Usando una expresión equivalente en , se obtiene que la condición de continuidad expresada por los limites de derecha e izquierda arriba, implica que

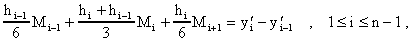
donde

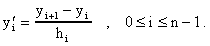
Tenemos aqui n-1 ecuaciones para las n+1 desconocidas .

Condición Natural de los Splines: Para fijar los dos grados de libertad en el spline, requerimos que s(x) sea lineal en los intervalos lo cual es equivalente a las condiciones . Tenemos ahora el siguiente sistema de ecuaciones Am=d para las restantes desconocidas donde:

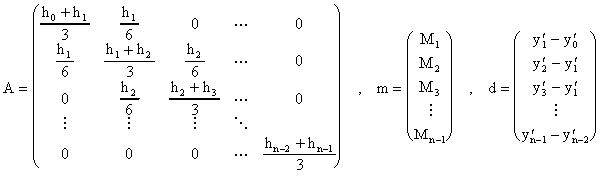
Note que la matriz de coeficientes de este sistema es tridiagonal y simétrica lo que hace que el spline s(x) pueda ser calculado en forma eficiente. El siguiente programa en MATLAB ensambla la matriz y lado derecho según definidos arriba y resuelve el sistema para determinar los M's:

%
% Los datos estan dados por los vectores x=[x(1) … x(n)] , y=[y(1) … y(n)]
%
n=length(x)
dx=x(2:n)-x(1:n-1);
yp=(y(2:n)-y(1:n-1))./dx;
a=sparse([1:n-2],[1:n-2],(dx(1:n-2)+dx(2:n-1))/3,n-2,n-2);
udiag=sparse([1:n-3],[2,n-2],dx(2:n-2)/6,n-2,n-2);
a=udiag'+a+udiag;
d=yp(2:n-1)-yp(1:n-2);
m=a\d;

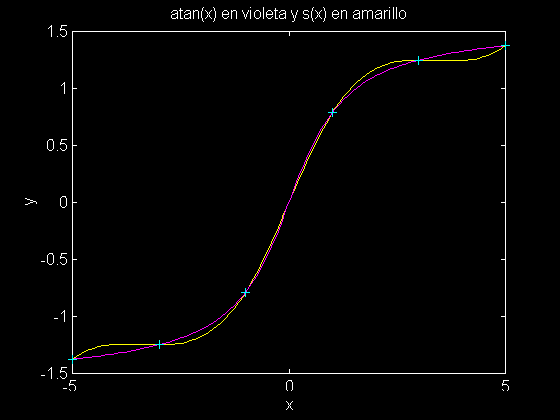
La función spline de MATLAB se utiliza para calcular el spline s(x) directamente. En el siguiente ejemplo los datos se obtienen dividiendo el intervalo [-5,5] en seis subintervalos y evaluamos la función atan (tangente inversa) en los puntos de la partición. Luego construimos el spline que interpola en estos puntos y lo graficamos:

%
% Divide el intervalo [-5,5] en cinco pedazos generando asi seis puntos
%
x=linspace(-5,5,6);
%
% Evalua la función atan en los puntos de la partición
%
y=atan(x);
%
% Calcula la representación del spline que interpola a los datos
%
pp=spline(x,y);
%
% Calcula 100 puntos en el intervalo [-5,5] para las graficas
%
z=linspace(-5,5,100);
%
% Evalua el spline y la función atan en los 100 puntos
%
sval=ppval(pp,z);
y1=atan(z);
%
% Grafica el spline, atan, y los puntos de interpolaci&oacuten en un mismo
% sistema de coordenadas
%
plot(z,sval,z,y1,x,y,'+')
xlabel('x');
ylabel('y');
title('atan(x) en violeta y s(x) en amarillo')