La convergencia lenta del método de Euler y lo restringido de su región de estabilidad absoluta nos lleva a considerar métodos de orden de convergencia mayor. En clase mencionamos que en cada paso el método de Euler se mueve a lo largo de la tangente de una cierta curva que esta "cerca" a la curva desconocida o buscada. Los métodos Runge-Kutta extienden esta idea geométrica al utilizar varias derivadas o tangentes intermedias, en lugar de solo una, para aproximar la función desconocida. Los métodos Runge-Kutta más simples se obtienen usando dos de estas derivadas intermedias.

Métodos Runge-Kutta de dos Evaluaciones: Aqui buscamos métodos o fórmulas numéricas de la forma:

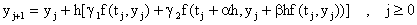
Note que apesar de que en la fórmula se perciven tres f's, el método envuelve solo dos evaluaciones ya que dos de estas f's tienen los mismos argumentos. La idea ahora es determinar los parámetros de modo que el método tenga orden de convergencia lo más alto posible. Un análisis del error local de esta fórmula basado en el Teorema de Taylor muestra que el orden más alto que puede tener esta fórmula es dos y que esto puede ocurrir si y solo si:

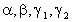
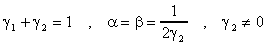
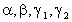
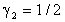Es decir si cumplen con estas condiciones, entonces e_j=y(t_j)-y_j=O(h²) para toda j. Algunos casos especiales de estas fórmulas son:

1. Método de Heun: Aqui se toma de modo que el método reduce a:

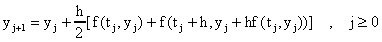
   Para propositos de hacer cálculos es mejor escribir esta fórmula como:

   
   
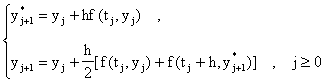
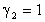2. Método del Punto Medio: Aqui se toma de modo que el método reduce a:

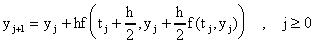
Veamos ahora una implementación en MATLAB del método de Heun. Note que en el ciclo "for" tenemos exactamente dos evaluaciones de "f". Tenemos pues:

function [tvals,yvals]=heun(f,t0,b,y0,h)
n=floor((b-t0)/h)+1;
m=length(y0);
k1=zeros(1,m);
tvals=zeros(n+1,1);
yvals=zeros(n+1,m);
index=[0:1:n]';
tvals=t0+h*index;
yvals(1,:)=y0;
h2=h/2;
for i=2:n+1
k1=feval(f,tvals(i-1), yvals(i-1,:));
yvals(i,:)=yvals(i-1,:)+h*k1;
yvals(i,:)=yvals(i-1,:)+h2*(k1+feval(f,tvals(i),yvals(i,:));
end

Ejemplo 1: Consideremos aqui las ecuaciones diferenciales que se obtienen de las leyes de Newton aplicadas al problema de dos cuerpos. Suponemos aqui que uno de los cuerpos es mucho más masivo que el otro de modo que su movimiento es descartable, e.g., la tierra y un satélite. Suponemos también que el movimiento es en un plano. Como la fuerza gravitacional es inversamente proporcional a la distancia entre los cuerpos, tenemos tomando todas las constantes envueltas como uno, que la posición (x(t),y(t)) del cuerpo pequeño esta dada por el sistema de ecuaciones diferenciales:

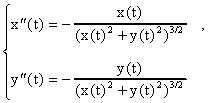
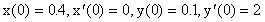
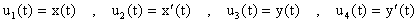
Tomamos como condiciones iniciales . Debido a que este es un sistema de orden dos, tenemos que hacer la sustitución:

lo cual tranforma el sistema de arriba al siguiente sistema de orden uno:

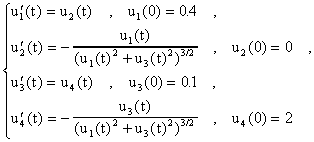
Definimos ahora la siguiente subrutina en MATLAB que evalua el lado derecho de este sistema:

function f=satelite(t,u)
f=zeros(1,4);
denom=(u(1)^2+u(3)^2)^1.5;
f(1)=u(2);
f(2)=-u(1)/denom;
f(3)=u(4);
f(4)=-u(3)/denom;

Ahora calculamos y graficamos la solución del problema de valor inicial con la siguiente secuencia de instrucciones en MATLAB. Note que graficamos el conjunto de puntos (x(t),y(t)) para los t's generados en lugar de (t,x(t)) y (t,y(t)). Tenemos pues:

[t,y]=heun('satelite',0,10,[0.4,0,0.1,2],0.01);
plot(y(:,1),y(:,3))
xlabel('X');ylabel('Y');
title('Solucion particular del problema de dos cuerpos')

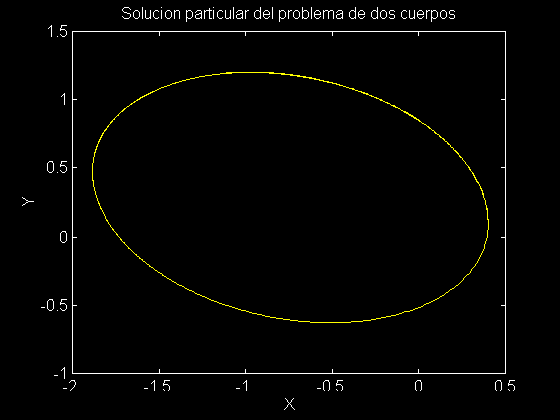
Note que la curva es efectivamente una elipse aunque esto se acentua en la gráfica por que los ejes tienen unidades de largo distintas. <>

Métodos Runge-Kutta de más de dos Evaluaciones: Aunque el método de Heun fué bastante efectivo en el ejemplo anterior, nos interesa encontrar métodos de orden aún más alto que no requieran h's muy pequeñas. Vimos aqui que un método Runge-Kutta de dos evaluaciones intermedias genera un método de orden dos. Es razonable pensar que tres o cuatro evaluaciones intermedias producen métodos Runge-Kutta de ordenes tres y cuatro respectivamente. Este el caso pero ya para cinco evaluaciones no obtenemos necesariamente métodos Runge-Kutta de orden cinco pero si con seis evaluaciones. Un ejemplo de un método Runge-Kutta de orden cuatro de cuatro evaluaciones es el llamado método Runge-Kutta clásico definido por las fórmulas:

MATLAB cuenta con dos subrutinas intrinsecas para la solución de problemas de valor inicial: ode23 y ode45. ode23 utiliza una combinación de un método Runge-Kutta de orden dos con otro de orden tres. La combinación de estos métodos permite el poder estimar el error en la aproximación numérica en cada paso y asi la subrutina puede ajustar el largo de paso "h" en forma dinámica para mantener el error global menor de una tolerancia especificada por el usuario. Estos métodos se dicen que son adaptativos ó de largo de paso variable. La subrutina ode45 es similar a ode23 pero utiliza una combinación de métodos de ordenes cuatro y cinco de cinco y seis evaluaciones respectivamente. La secuencia de llamada de ambas rutinas es idéntica y requiere del nombre de la función f, los tiempos inicial y final, la condición inicial, la tolerancia para los computos, y un indicador de si la rutina imprime o no los resultados calculados en la ventana de MATLAB. Normalmente este indicador se toma como cero que es su valor por omisión. Por ejemplo un computo similar al del Ejemplo 1 lo podemos realizar remplazando la llamada a Heun por:

[t,y]=ode23('satelite',0,10,[0.4,0,0.1,2],0.0001);

donde la solución se calcula con un error global de 0.0001. La misma instrucción con ode45 produce la gráfica:

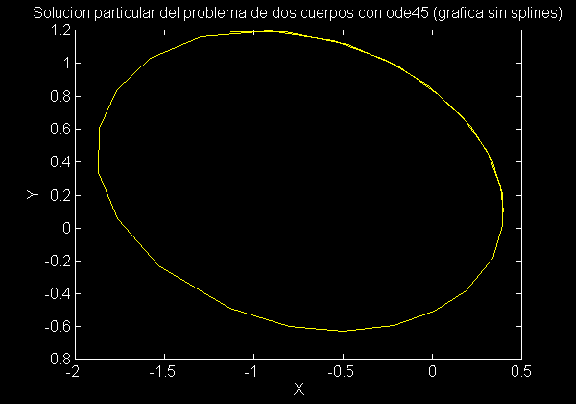
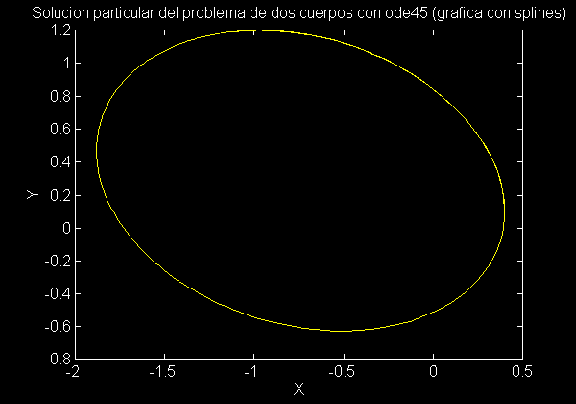
Las esquinas en esta gráfica se deben a que como ode45 usa un método de orden mayor, esto le permite dar pasos más largos en "t" lo que al graficar produce las esquinas. Este trazado lo podemos mejorar usando splines cúbicos como sigue:

[t,y]=ode45('satelite',0,10,[0.4,0,0.1,2],0.0001);
tt=linspace(0,10,200);
xx=spline(t,y(:,1),tt);
yy=spline(t,y(:,3),tt);
plot(xx,yy)
xlabel('X');ylabel('Y');
title('Solucion particular del problema de dos cuerpos con ode45 (grafica con splines)')

lo cual resulta en la mejor gráfica:

Ejercicios:

1. Resuelva el siguiente problema de valor inicial usando las subrutinas ode23 o ode45:
   

   donde y
   

   

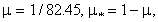
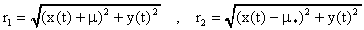
   Examine los efectos en los cálculos de la tolerancia especificada por el usuario. Grafique las soluciones calculadas como funciones de "t" y en el plano x-y.
   

2. Las ecuaciones de Lorenz estan dadas por el siguiente sistema de ecuaciones diferenciales:
   

   donde s, r, b son parámetros del sistema. Usando ode45 con una tolerancia de 0.000005 resuelva las ecuaciones de Lorenz para s=10, r=126.52, b=8/3 con las condiciones iniciales x(0)=-7.69, y(0)=-15.61, z(0)=90.39. Grafique las soluciones calculadas como funciones de t. Grafique las soluciones x(t), z(t) en el plano x-z. Para los valores de s, r, b dados el sistema de Lorenz posee lo que se conoce como comportamiento "caótico".